358
471
всего разделов:
активных пользователей:
30 мартра 2005
Форумы снова функционируют.
21 декабря 2004
Видимо в связи с обнаруженными дырами в phpBB, форум был взломан, а через него взломано и всё остальное содержимое ceemat.ru. Всё кроме форума восстановлено, ведется дискуссия по поводу его сохранения.
Приносим извинения за неудобства.
29 сентября 2004
Форум обновился до версии 2.0.10
15 мая 2004
Новый раздел: "Программирование"
16 апреля 2004 года
Задачи Ярославского турнира математических боев — 124 задачи с решениями.
29 марта 2004
Таллинская викторина: занимательные вопросы и задачи для увлеченных химией.
Первая лига (8)
В прямоугольнике выбрана произвольная точка (внутри или на границе) и соединена отрезками с вершинами прямоугольника. Докажите, что из этих четырех отрезков найдутся три, из которых можно составить треугольник. |
Докажем, что из отрезков BM, CM и DM можно составить треугольник. Для этого достаточно убедиться, что сумма любых двух из этих отрезков больше третьего. Заметим, что CM > BM, потому что точка B лежит по ту же сторону от перпендикуляра к середине отрезка BC, что и точка M. Тогда CM + DM > BM. Аналогично, CM + BM > DM. Неравенство BM + DM > CM следует из цепочки неравенств: BM + DM ³ BD = CA ³ CM. Если хотя бы одно из неравенств является строгим, то BM + DM > CM. Оба неравенства не могут обращаться в равенства. Действительно, равенство BM + DM = BD выполняется, если точка M лежит на отрезке BD, а равенство CA = CM — если точка M совпадает с точкой A. Но точка A не лежит на отрезке BD, так что одновременное выполнение обоих равенств невозможно. |
Авторы: Е. Барабанов, И. Воронович. |
28 Февраля 2004 22:43 Раздел каталога :: Ссылка на задачу
|
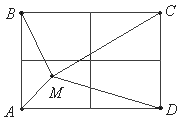Обозначим вершины прямоугольника точками A, B, C и D, и проведем два отрезка, соединяющих середины противоположных сторон данного прямоугольника. Эти отрезки разобьют прямоугольник на четыре равных прямоугольника. Пусть для определенности выбранная произвольная точка M принадлежит тому прямоугольнику (возможно, его границе), одна из вершин которого совпадает с точкой A.