358
471
всего разделов:
активных пользователей:
30 мартра 2005
Форумы снова функционируют.
21 декабря 2004
Видимо в связи с обнаруженными дырами в phpBB, форум был взломан, а через него взломано и всё остальное содержимое ceemat.ru. Всё кроме форума восстановлено, ведется дискуссия по поводу его сохранения.
Приносим извинения за неудобства.
29 сентября 2004
Форум обновился до версии 2.0.10
15 мая 2004
Новый раздел: "Программирование"
16 апреля 2004 года
Задачи Ярославского турнира математических боев — 124 задачи с решениями.
29 марта 2004
Таллинская викторина: занимательные вопросы и задачи для увлеченных химией.
Вторая лига (8)
| Страницы: 1 2 » | |
1. | Целые числа х, у, z таковы, что xy + yz + xz = 1. Докажите, что число (1 + x2)(1 + y2)(1 + z2) является полным квадратом. |
25 Февраля 2004 22:55 | |
2. | В треугольнике АВС точка M — середина отрезка ВС, точка N — середина отрезка АС, точка K — середина отрезка AN. Отрезки ВN и МК пересекаются в точке О, причем ÐВОМ = ÐОКN. Докажите равенство AC = BN. |
25 Февраля 2004 23:05 | |
3. |
Докажите равенство площадей четырехугольников ALCN и KBMD. |
25 Февраля 2004 22:56 | |
4. | Архипелаг состоит из 7 островов вблизи материка. С каждого острова выходят три моста. Между любыми двумя островами, а также между каждым островом и материком имеется не более одного моста. Из острова Чунга на остров Чанга переехать нельзя. Сколько мостов связывают острова архипелага с материком? |
25 Февраля 2004 23:06 | |
5. | В выпуклом 12-угольнике все углы кратны 30 градусам. Докажите, что все углы этого многоугольника равны. |
25 Февраля 2004 23:08 | |
| Страницы: 1 2 » | |
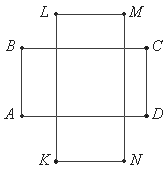Прямоугольники ABCD и KLMN имеют соответственно параллельные стороны и расположены, как показано на рисунке.