358
476
всего разделов:
активных пользователей:
30 мартра 2005
Форумы снова функционируют.
21 декабря 2004
Видимо в связи с обнаруженными дырами в phpBB, форум был взломан, а через него взломано и всё остальное содержимое ceemat.ru. Всё кроме форума восстановлено, ведется дискуссия по поводу его сохранения.
Приносим извинения за неудобства.
29 сентября 2004
Форум обновился до версии 2.0.10
15 мая 2004
Новый раздел: "Программирование"
16 апреля 2004 года
Задачи Ярославского турнира математических боев — 124 задачи с решениями.
29 марта 2004
Таллинская викторина: занимательные вопросы и задачи для увлеченных химией.
Юниорская лига (8)
| Страницы: 1 | |
1. | У 5 ключей от гостиничных номеров потерялись бирки. За какое наименьшее число пробных открываний можно наверняка определить, от какого номера каждый ключ? |
17 Февраля 2004 17:58 | |
2. | Матрос Фукс купил цифровые часы. Выяснилось, однако, что они настроены на туземное 24-часовое время, которое отстает от московского на целое число минут, и перенастроить их нельзя. Заметив, что все цифры, кроме 3, 4, 7, в перевернутом виде тоже выглядят как цифры, капитан Врунгель поставил часы вверх ногами (так что, например, вместо O52I видно I25O ). Оказалось, что теперь часы ровно 6 раз в сутки правильно показывают московское время. На сколько туземное время отстает от московского? |
17 Февраля 2004 17:58 | |
3. | Можно ли раскрасить натуральный ряд в 4 цвета так, чтобы для любого натурального n числа n, 2n, 3n и 4n были окрашены в разные цвета? |
17 Февраля 2004 17:59 | |
4. | За один ход разрешается отсечь от многоугольника треугольник прямой, не проходящей через вершины многоугольника. Вначале есть квадрат с точкой в центре. Докажите, что после любого числа ходов точка не будет отсечена. |
17 Февраля 2004 17:59 | |
5. | Во вписанном четырехугольнике ABCD точка K — середина стороны AD, а ÐABK = ÐDCK. Докажите, что AB = CD. |
17 Февраля 2004 18:00 | |
6. | Пусть a и n — натуральные числа. Известно, что последняя цифра суммы a + a2 + … + an равна 1. Докажите, что последние цифры чисел a и n тоже равны 1. |
17 Февраля 2004 18:00 | |
7. | Можно ли ребра куба раскрасить в два цвета так, чтобы можно было добраться от любой вершины к любой другой как по ребрам одного цвета, так и по ребрам другого цвета? |
17 Февраля 2004 18:01 | |
8. | Известно, что a > b > 0 и
|
17 Февраля 2004 18:02 | |
| Страницы: 1 | |
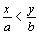 .
Докажите, что
.
Докажите, что 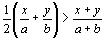 .
.