358
476
всего разделов:
активных пользователей:
30 мартра 2005
Форумы снова функционируют.
21 декабря 2004
Видимо в связи с обнаруженными дырами в phpBB, форум был взломан, а через него взломано и всё остальное содержимое ceemat.ru. Всё кроме форума восстановлено, ведется дискуссия по поводу его сохранения.
Приносим извинения за неудобства.
29 сентября 2004
Форум обновился до версии 2.0.10
15 мая 2004
Новый раздел: "Программирование"
16 апреля 2004 года
Задачи Ярославского турнира математических боев — 124 задачи с решениями.
29 марта 2004
Таллинская викторина: занимательные вопросы и задачи для увлеченных химией.
Высшая лига (10)
| Страницы: 1 | |
1. | У N ключей от гостиничных номеров потерялись бирки. За какое наименьшее число пробных открываний можно наверняка определить, от какого номера каждый ключ? |
17 Февраля 2004 13:50 | |
2. | Даны 6 точек в пространстве, никакие 4 из которые не лежат на одной плоскости. Докажите, что их можно разбить на две тройки так, что контуры двух треугольников с вершинами в точках каждой из троек будут зацеплены. |
17 Февраля 2004 13:53 | |
3. | Даны 6 точек в пространстве, никакие 4 из которые не лежат на одной плоскости. Докажите, что их можно разбить на две тройки так, что контуры двух треугольников с вершинами в точках каждой из троек будут зацеплены. |
17 Февраля 2004 17:44 | |
4. | Дан остроугольный треугольник ABC и точка M внутри него.
Длины сторон треугольника равняются a, b и c.
|
17 Февраля 2004 17:45 | |
5. | Существует ли убывающая последовательность
x(1), x(2), …, x(n), … положительных чисел,
удовлетворяющая при всех n > 1 условию
|
17 Февраля 2004 16:04 | |
6. | Можно ли раскрасить натуральный ряд в 6 цветов так, чтобы для любого натурального n числа n, 2n, …, 6n окрашены в разные цвета? |
17 Февраля 2004 16:06 | |
7. | Из двух разных прямоугольников один назовем меньшим, если его можно поместить внутрь второго, причем его стороны будут параллельны сторонам второго прямоугольника. Из некоторого прямоугольного листа бумаги (заготовки) вырезали несколько прямоугольников со сторонами, параллельными сторонам исходного прямоугольника. Затем каждый из вырезанных прямоугольников уменьшили. Всегда ли можно было для получения этого "уменьшенного" набора обойтись меньшей заготовкой? |
17 Февраля 2004 17:33 | |
8. | В выпуклом пятиугольнике ABCDE на диагонали BD нашлась такая точка M, что ÐCBD = ÐMEA, ÐCDB = ÐMAE. Докажите, что SABDE = SACE. |
17 Февраля 2004 17:39 | |
9. | Подряд выписываются числа 1, 2, …, n. Существует ли такое n, что полученное число делится на 137? |
17 Февраля 2004 17:34 | |
10. | Дан единичный круг и фиксировано число d < 2. Двое играющих по очереди проводят в этом круге отрезки без концов длины d, не имеющие общих точек с ранее проведенными. Проигрывает тот, кто не может сделать хода. Может ли кто-нибудь из них выиграть независимо от игры противника? |
17 Февраля 2004 17:35 | |
| Страницы: 1 | |
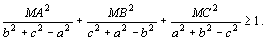 .
.