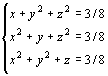Вторая лига (8)

1.

Есть веревочная сетка в виде квадрата 8 × 8, разбитого на ячейки 1 × 1. Какую самую длинную веревку можно из нее вырезать? (От узлов можно отрезать любой конец не нарушая соединения остальных, но нельзя разрезать узел так, чтобы концов не образовалось).

2.

Два игрока по очереди делают ходы в следующей игре: первый ставит на шахматную доску ладью, второй передвигает ее ходом коня, первый передвигает ее ходом слона, затем второй снова — ходом коня и т.д. Ставить ладью на клетку, на которой она уже была, запрещено. Проигрывает не имеющий хода. Кто выиграет при правильной игре?

3.

Натуральные числа 1, 2, …, 100 содержатся в объединении N геометрических прогрессий. Докажите, что N ³ 25.

4.

Докажите неравенство:
(a + 2b + 3c)² £ 2(a² + 4b² + 9c²) + 8ab.

5.

Решите в вещественных числах систему уравнений:

6.

Параллелограмм разрезан на несколько выпуклых многоугольников. Докажите, что один из них можно накрыть всеми остальными вместе.

7.

Несколько телефонов соединены проводами так, что каждый провод соединяет 2 телефона и каждая пара телефонов соединена не более чем одним проводом. Из каждого телефона ведет 3 провода. Верно ли, что провода всегда можно покрасить в 3 цвета так, что от каждого телефона отходили 3 провода разных цветов.

8.

На сторонах AB и BC остроугольного треугольника ABC как на диаметрах во внешнюю сторону построены полуокружности S₁ и S₂ соответственно. Продолжения высот треугольника ABC, опушенных из вершин C и A пересекаются с полуокружностями S₁ и S₂ в точках E и F соответственно. Докажите, что BE = BF.