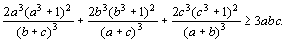358
476
всего разделов:
активных пользователей:
30 мартра 2005
Форумы снова функционируют.
21 декабря 2004
Видимо в связи с обнаруженными дырами в phpBB, форум был взломан, а через него взломано и всё остальное содержимое ceemat.ru. Всё кроме форума восстановлено, ведется дискуссия по поводу его сохранения.
Приносим извинения за неудобства.
29 сентября 2004
Форум обновился до версии 2.0.10
15 мая 2004
Новый раздел: "Программирование"
16 апреля 2004 года
Задачи Ярославского турнира математических боев — 124 задачи с решениями.
29 марта 2004
Таллинская викторина: занимательные вопросы и задачи для увлеченных химией.
Высшая лига (10)
| Страницы: 1 2 » | |
1. | Докажите, что для любых натуральных чисел a и b существует натуральное число n такое, что an + bn+1 — составное число. |
16 Февраля 2004 22:45 | |
2. | В графе 2000 вершин степени 3. Известно, что количество способов раскрасить его ребра в 3 цвета так, чтобы из каждой вершины выходило ровно по одному ребру каждого цвета, не делится на 4. Докажите, что в этом графе существует гамильтонов цикл (то есть цикл, проходящий по каждой вершине один раз). |
16 Февраля 2004 22:45 | |
3. | Пусть a, b, c — положительные числа. Докажите неравенство:
|
16 Февраля 2004 22:47 | |
4. | Существует ли такой выпуклый 1999-угольник, на сторонах которого (в порядке обхода) лежат соответственно 1, 2, …, 1999 точек с целыми координатами? |
16 Февраля 2004 22:47 | |
5. | Числовая последовательность {xn} задана условиями: x1 = a, xn+1 = (2xn – 1)2 для n ³ 1. Докажите, что в любом интервале (α, β) из отрезка [0, 1] найдется такое a, для которого все члены последовательности, начиная с некоторого равны. |
16 Февраля 2004 22:49 | |
| Страницы: 1 2 » | |