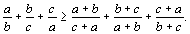Первая лига (10)

1.

Докажите, что для любых положительных чисел a, b, c выполняется неравенство

2.

Между волейбольными командами двух стран был проведен матч-турнир, в котором каждая команда сыграла ровно по одному разу со всеми командами другой страны. При этом каждая команда выиграла хотя бы одну встречу. Докажите, что найдутся четыре команды A, B, C и D такие, что A выиграла у B, B выиграла у C, С выиграла у D, а D выиграла у A. (Ничьих в волейболе не бывает)

3.

Имеется 6 одинаковых по виду гирек с массой 1, 2, 3, 4, 5, 6 граммов. На гирьках сделали надписи "1", "2", "3", "4", "5", "6". Можно ли за 2 взвешивания на чашечных весах без гирь проверить, что надписи сделаны без ошибок?

4.

Будем говорить, что несколько супружеских пар не образуют "устойчивого сообщества", если среди них можно указать мужчину и женщину, которые не состоят в браке, но нравятся друг другу больше, чем их законные супруги. Пусть теперь есть 99 юношей и 99 девушек, где каждый из юношей составил список, в котором расположил всех девушек в порядке убывания "предпочтений", и аналогично поступили все девушки. Докажите, что руководствуясь этими списками, всегда возможно составить из них 99 супружеских пар, образующих "устойчивое сообщество".

5.

В какое наименьшее число цветов можно раскрасить шахматную доску 100 × 100 так, чтобы каждая клетка граничила по стороне с клеткой другого цвета, и между любыми двумя клетками одного цвета ладья могла пройти по клеткам того же цвета (не перепрыгивая через другой цвет)?

6.

Пятизначное число с суммой цифр 37 делится на 37. Докажите, что его третья цифра — 9.

7.

Есть многочлен третьей степени
P(x) = x³ + ax² + bx + c.
Известно, что если x — целое, то P(x) — куб целого числа.

Докажите, что P(x) º (x + d)³ при некотором d.

8.

Всякий ли параллелепипед имеет в сечении прямоугольник?

9.

Каждая грань куба со стороной 3 разбита на клетки 1 × 1. Поверхность куба удалось оклеить семнадцатью бумажными полосками 3 × 1 и одним уголком так, что каждая полоска и уголок закрыли по 3 целые клетки (возможно, с перегибанием через ребро). Найти все возможные расположения уголка.

10.

В четырехугольнике ABCD AB = AD и CB = CD, ÐBAD = 120°, ÐBCD = 60°. На стороне BC выбрана точка M, а на стороне CD — точка N, так что MN касается окружности с центром в точке A радиуса AB. Докажите, что диагональ BD делит площадь треугольника AMN в отношении 1 : 3.