358
476
всего разделов:
активных пользователей:
30 мартра 2005
Форумы снова функционируют.
21 декабря 2004
Видимо в связи с обнаруженными дырами в phpBB, форум был взломан, а через него взломано и всё остальное содержимое ceemat.ru. Всё кроме форума восстановлено, ведется дискуссия по поводу его сохранения.
Приносим извинения за неудобства.
29 сентября 2004
Форум обновился до версии 2.0.10
15 мая 2004
Новый раздел: "Программирование"
16 апреля 2004 года
Задачи Ярославского турнира математических боев — 124 задачи с решениями.
29 марта 2004
Таллинская викторина: занимательные вопросы и задачи для увлеченных химией.
Призовые задачи (20)
| Страницы: 1 | |
1. |
|
17 Февраля 2004 20:28 | |
2. | От трехзначного числа отняли сумму кубов его цифр. Какой наибольший результат мог при этом получиться? |
17 Февраля 2004 20:31 | |
3. | AH и CP — высоты треугольника АВС. Какой может быть величина угла В, если известно, что АС = 2НР? |
17 Февраля 2004 20:31 | |
4. | Обозначим через S(n) сумму цифр числа n.
Найдите наименьшее натуральное число n, для которого
|
17 Февраля 2004 20:32 | |
5. | Сколько различных целочисленных решений имеет неравенство |x| + |y| < 1999? |
17 Февраля 2004 20:33 | |
6. | В стаде 10 коров. Первая может съесть стог сена за 1 день,
вторая — за 2 дня, третья — за 3 дня, …, десятая — за 10 дней.
|
17 Февраля 2004 20:34 | |
7. | В однокруговом волейбольном турнире (без ничьих) участвовало 23 команды.
|
17 Февраля 2004 20:35 | |
8. | Решите в натуральных числах уравнение
|
17 Февраля 2004 20:36 | |
9. | Банкир Петя ежедневно выходит из дома на работу в 8 утра, на улице его встречает автомобиль и отвозит на работу. Однажды он вышел из дома раньше и пошел навстречу машине. Благодаря этому Петя приехал на работу на 20 минут раньше, чем обычно. Определите, в какое время Петя сел в этот день в автомобиль? |
17 Февраля 2004 20:37 | |
10. | Дан квадрат со стороной 1. Найдите геометрическое место точек плоскости, сумма расстояний которых до сторон квадрата или его продолжений равна 4. |
17 Февраля 2004 20:38 | |
11. | Найдите все натуральные числа n такие, что (n – 1)! не делится на n2. |
17 Февраля 2004 20:39 | |
12. | В циферблат часов добавили стрелку, которая в любой момент времени образует равные углы с часовой и минутной стрелками (идет по биссектрисе угла). Сколько полных оборотов делает эта стрелка в течение суток? |
17 Февраля 2004 20:40 | |
13. | На потолке комнаты сидит муха. Расстояние от нее до трех из четырех нижних углов комнаты равно 3м, 4м и 5м. Чему равно расстояние от мухи до четвертого нижнего угла, если известно, что оно больше всех остальных? |
17 Февраля 2004 20:49 | |
14. | Назовем натуральное число хорошим, если оно представимо в виде суммы двух
трехзначных чисел |
17 Февраля 2004 20:50 | |
15. | Сколько корней имеет уравнение sinx = x/31? |
17 Февраля 2004 20:51 | |
16. | В турнире каждый шахматист, не занявший одно из трех последних мест, половину своих очков набрал во встречах с участниками, занявшими три последних места. (Занявший третье место с конца набрал очков меньше, чем четвертый с конца). Сколько человек приняло участие в турнире? |
17 Февраля 2004 20:52 | |
17. | Решите систему уравнений
|
17 Февраля 2004 20:52 | |
18. |
Чему равна площадь заштрихованной части фигуры? |
17 Февраля 2004 20:54 | |
19. | Сколькими способами можно представить число 100 в виде суммы трех натуральных слагаемых (представления, отличающиеся только порядком слагаемых, считаются одинаковыми)? |
17 Февраля 2004 20:55 | |
20. | Найдите все четырехзначные числа, всякая натуральная степень которых оканчивается на 4 цифры, составляющие исходное число. |
17 Февраля 2004 20:55 | |
| Страницы: 1 | |
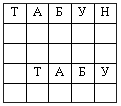 Завершите заполнение квадрата буквами Т, А, Б, У, Н так, чтобы в каждой строке,
каждом столбце и каждой из двух диагоналей квадрата эти буквы встречались по
одному разу.
Завершите заполнение квадрата буквами Т, А, Б, У, Н так, чтобы в каждой строке,
каждом столбце и каждой из двух диагоналей квадрата эти буквы встречались по
одному разу.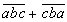 ,
(a и с не равны 0). Сколько существует хороших чисел?
,
(a и с не равны 0). Сколько существует хороших чисел?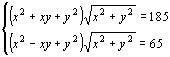 .
.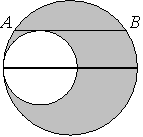 Отрезок АВ параллелен каждому из диаметров полукругов, расположенных так, как показано на рисунке, касается меньшего полукруга и равен 10см.
Отрезок АВ параллелен каждому из диаметров полукругов, расположенных так, как показано на рисунке, касается меньшего полукруга и равен 10см.