358
476
всего разделов:
активных пользователей:
30 мартра 2005
Форумы снова функционируют.
21 декабря 2004
Видимо в связи с обнаруженными дырами в phpBB, форум был взломан, а через него взломано и всё остальное содержимое ceemat.ru. Всё кроме форума восстановлено, ведется дискуссия по поводу его сохранения.
Приносим извинения за неудобства.
29 сентября 2004
Форум обновился до версии 2.0.10
15 мая 2004
Новый раздел: "Программирование"
16 апреля 2004 года
Задачи Ярославского турнира математических боев — 124 задачи с решениями.
29 марта 2004
Таллинская викторина: занимательные вопросы и задачи для увлеченных химией.
Призовые задачи (20)
| Страницы: 1 2 » | |
1. |
|
17 Февраля 2004 20:28 | |
2. | От трехзначного числа отняли сумму кубов его цифр. Какой наибольший результат мог при этом получиться? |
17 Февраля 2004 20:31 | |
3. | AH и CP — высоты треугольника АВС. Какой может быть величина угла В, если известно, что АС = 2НР? |
17 Февраля 2004 20:31 | |
4. | Обозначим через S(n) сумму цифр числа n.
Найдите наименьшее натуральное число n, для которого
|
17 Февраля 2004 20:32 | |
5. | Сколько различных целочисленных решений имеет неравенство |x| + |y| < 1999? |
17 Февраля 2004 20:33 | |
6. | В стаде 10 коров. Первая может съесть стог сена за 1 день,
вторая — за 2 дня, третья — за 3 дня, …, десятая — за 10 дней.
|
17 Февраля 2004 20:34 | |
7. | В однокруговом волейбольном турнире (без ничьих) участвовало 23 команды.
|
17 Февраля 2004 20:35 | |
8. | Решите в натуральных числах уравнение
|
17 Февраля 2004 20:36 | |
9. | Банкир Петя ежедневно выходит из дома на работу в 8 утра, на улице его встречает автомобиль и отвозит на работу. Однажды он вышел из дома раньше и пошел навстречу машине. Благодаря этому Петя приехал на работу на 20 минут раньше, чем обычно. Определите, в какое время Петя сел в этот день в автомобиль? |
17 Февраля 2004 20:37 | |
10. | Дан квадрат со стороной 1. Найдите геометрическое место точек плоскости, сумма расстояний которых до сторон квадрата или его продолжений равна 4. |
17 Февраля 2004 20:38 | |
| Страницы: 1 2 » | |
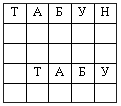 Завершите заполнение квадрата буквами Т, А, Б, У, Н так, чтобы в каждой строке,
каждом столбце и каждой из двух диагоналей квадрата эти буквы встречались по
одному разу.
Завершите заполнение квадрата буквами Т, А, Б, У, Н так, чтобы в каждой строке,
каждом столбце и каждой из двух диагоналей квадрата эти буквы встречались по
одному разу.