358
476
всего разделов:
активных пользователей:
30 мартра 2005
Форумы снова функционируют.
21 декабря 2004
Видимо в связи с обнаруженными дырами в phpBB, форум был взломан, а через него взломано и всё остальное содержимое ceemat.ru. Всё кроме форума восстановлено, ведется дискуссия по поводу его сохранения.
Приносим извинения за неудобства.
29 сентября 2004
Форум обновился до версии 2.0.10
15 мая 2004
Новый раздел: "Программирование"
16 апреля 2004 года
Задачи Ярославского турнира математических боев — 124 задачи с решениями.
29 марта 2004
Таллинская викторина: занимательные вопросы и задачи для увлеченных химией.
Весна 2001 года (25)
| Страницы: 1 | |
1. | Как от куска шнура длиной 2/3 метра отрезать ровно полметра, не имея измерительного инструмента? Ответ пояснить. |
8 Февраля 2004 20:18 | |
2. | На озере цветет одна лилия. Каждый день число цветков удваивается, а на 20-й день все озеро покрылось цветками. На который день покрылась цветами половина озера? |
8 Февраля 2004 20:20 | |
3. | Девочка заменила в своем имени каждую букву ее номером в русском алфавите и получила число 2011533. Как ее зовут? Ответ пояснить. |
8 Февраля 2004 20:21 | |
4. | Имеется три сосуда без делений объемами 4л, 5л и 6л, кран с водой, раковина и 4л сиропа в самом маленьком сосуде. Можно ли с помощью переливаний получить 8л смеси воды с сиропом так, чтобы в каждом сосуде воды и сиропа было поровну. |
8 Февраля 2004 20:22 | |
5. | На 20 карточках написаны натуральные числа от 1 до 20. Из этих карточек составили 10 дробей. Какое наибольшее число этих дробей может иметь целые значения? (Указать количество дробей и доказать, что большее количество получить нельзя.) |
8 Февраля 2004 20:22 | |
6. | Офеня купил на оптовом рынке партию ручек и предлагает покупателям либо одну ручку за 5 рублей, либо три ручки за 10 рублей. Офеня от каждого покупателя получает одинаковую прибыль. Какова оптовая цена ручки? |
8 Февраля 2004 20:22 | |
7. | Из кубика Рубика 3 × 3 × 3 удалили центральный кубик и восемь угловых кубиков. Можно ли оставшуюся фигуру из 18 маленьких кубиков составить из шести брусков размером 3 × 1 × 1? |
8 Февраля 2004 20:23 | |
8. | В записи 9, *, *, *, *, *, *, 7 замените звездочки числами так, чтобы сумма любых трех подряд стоящих чисел была равна 20. |
8 Февраля 2004 20:24 | |
9. | Три путешественника остановились на ночлег, имея мешок сухарей. Ночью один съел 1/3 всех сухарей, второй — 1/3 от того, что осталось, третий — 1/3 от оставшихся. Осталось 8 сухарей. Сколько сухарей было первоначально? |
8 Февраля 2004 20:24 | |
10. | Инопланетянин со звезды Тау Кита, прилетев на Землю в понедельник, воскликнул «А!». Во вторник он воскликнул «АУ!», в среду — «АУУА!», в четверг — «АУУАУААУ!». Что он воскликнет в субботу? |
8 Февраля 2004 20:25 | |
11. | Найдите все пятизначные числа, обладающие следующим свойством: каждая цифра числа больше суммы цифр, стоящих правее нее (первая цифра больше суммы 2, 3, 4, и 5-ой цифр, вторая цифра больше суммы 3, 4 и 5-ой цифр и т.д.) |
8 Февраля 2004 20:26 | |
12. | Для нумерации страниц книги потребовалось 2322 цифры. Сколько страниц содержит книга? |
8 Февраля 2004 20:27 | |
13. | Петя проснулся в восьмом часу утра и заметил, что часовая стрелка его будильника делит пополам угол между минутной стрелкой и стрелкой звонка, показывающей на цифру 8. Через какое время должен прозвенеть звонок? |
8 Февраля 2004 20:27 | |
14. | Имеются купюры достоинством в 3 и 5 рублей. а) Сколькими способами с помощью этих купюр можно разменять 15 рублей? б) Докажите, что n рублей разменивается меньшим числом способов, чем n + 15 рублей. (n — любое натурально число, большее 7.) |
8 Февраля 2004 20:31 | |
15. | Есть ровно четыре способа разменять А рублей, имея только купюры в 3 и 5 рублей. Чему может быть равно А? (Укажите все варианты и докажите, что других нет.) |
8 Февраля 2004 20:32 | |
16. | Автобусный билет считается счастливым, если между всеми его цифрами можно расставить знаки четырех арифметических действий и скобки так, чтобы значение полученного выражения равнялось 100. Является ли счастливым билет № 123456? |
8 Февраля 2004 20:33 | |
17. | В магазин привезли 223 литра молока в бидонах по 10 и 17 литров. Сколько было бидонов? |
8 Февраля 2004 20:34 | |
18. | У Коли на дне рождения было 5 друзей. Первому он отрезал 1/6 часть пирога, второму — 1/5 остатка, третьему — 1/4 того, что осталось, четвертому — 1/3 нового остатка. Последний кусок Коля разделил пополам с пятым другом. Кому достался самый большой кусок? |
8 Февраля 2004 20:34 | |
19. | Наташа и Инна купили по одинаковой коробке чая в пакетиках. Известно, что одного пакетика хватает на две или на три чашки чая. Наташа использовала всю коробку, выпив 41 чашку чая, а Инна — выпив 58 чашек. Сколько пакетиков было в коробке? |
8 Февраля 2004 20:35 | |
20. | Может ли горящая в комнате свеча не освещать полностью ни одну из ее шести стен, если свет распространяется прямолинейно? Ответ пояснить. |
8 Февраля 2004 20:36 | |
21. |
|
8 Февраля 2004 20:37 | |
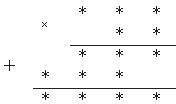
22. | Можно ли вместо звездочек вставить нечетные цифры так, чтобы равенство стало верным?
|
8 Февраля 2004 20:37 | |
23. | На двух параллельных прямых расположены точки: на одной — 4, на второй — 9. Сколько существует треугольников с вершинами в этих точках? |
8 Февраля 2004 20:38 | |
24. | а) Укажите два последовательных натуральных числа, сумма цифр каждого из которых делится на 17. б) Найдите наименьшее натуральное число, сумма цифр которого делится на 17, и сумма цифр следующего за ним числа тоже делится на 17. Укажите число и докажите, что меньшего числа нет. |
8 Февраля 2004 20:39 | |
25. | Из одного числа можно получать другое по следующему закону: сумму цифр числа умножать на 2. Например, из числа 2 можно получить последовательность: 2, 4, 8, 16, 14, 10, 2. а) Найдите все натуральные числа, переходящие сами в себя по этому закону. б) Докажите, что число 22001 после нескольких переходов по этому закону станет однозначным. |
8 Февраля 2004 20:39 | |
| Страницы: 1 | |
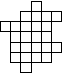 Сколькими способами можно разрезать
фигуру, изображенную на рисунке, на 6 равных частей, делая разрезы по линиям
сетки?
Сколькими способами можно разрезать
фигуру, изображенную на рисунке, на 6 равных частей, делая разрезы по линиям
сетки?