358
475
всего разделов:
активных пользователей:
30 мартра 2005
Форумы снова функционируют.
21 декабря 2004
Видимо в связи с обнаруженными дырами в phpBB, форум был взломан, а через него взломано и всё остальное содержимое ceemat.ru. Всё кроме форума восстановлено, ведется дискуссия по поводу его сохранения.
Приносим извинения за неудобства.
29 сентября 2004
Форум обновился до версии 2.0.10
15 мая 2004
Новый раздел: "Программирование"
16 апреля 2004 года
Задачи Ярославского турнира математических боев — 124 задачи с решениями.
29 марта 2004
Таллинская викторина: занимательные вопросы и задачи для увлеченных химией.
Осень 2000 года (25)
| Страницы: 1 | |
1. | На доске написано число 458. За один ход можно либо удвоить имеющееся число, либо стереть последнюю цифру. Как за несколько ходов получить число 14? |
5 Февраля 2004 22:01 | |
2. | Сколькими способами можно представить число 50 в виде суммы двух четных положительных чисел? (Представления считаются совпадающими, если они различаются лишь порядком слагаемых.) |
5 Февраля 2004 22:04 | |
3. | Цена картофеля повысилась на 20%. Через некоторое время цена понизилась на 20%. Когда картофель стоил дешевле: до повышения или после снижения? Ответ поясните. |
5 Февраля 2004 22:06 | |
4. | Используя семь двоек и знаки математических действий, несложно получить выражение, значение которого равно 2000: 2222 – 222. Можно ли, используя шесть пятерок, знаки математических действий: «+», «–», «×», «:» и скобки, получить выражение, значение которого равно 2000? |
5 Февраля 2004 22:07 | |
5. | Можно ли написать на гранях кубика числа 1, 2, 3, 4, 5, 6 (каждое число встречается один раз) так, чтобы числа на соседних гранях отличались не более чем на 2? |
5 Февраля 2004 22:08 | |
6. | В примере 123 × 567 + 29259 = 99 потерялись десятичные запятые в записи чисел. Как могли стоять запятые? |
5 Февраля 2004 22:08 | |
7. | Три мыши за 2 часа растаскивают по своим норам три мешка зерна. Сколько растаскивают мешков шесть мышей за 5 часов? |
5 Февраля 2004 22:09 | |
8. | Можно ли буквы Р, О, Б заменить цифрами (причем одинаковые буквы равными цифрами, а разные — неравными), чтобы число БОР было больше числа ОРБ, число ОРБ было больше числа РОБ, а число РОБ — больше числа БРО? |
5 Февраля 2004 22:12 | |
9. | Есть три человека А, В и С, про которых известно, что один из них рыцарь (всегда говорит правду), другой — лжец (всегда врет), а третий — нормальный человек, который может и говорить правду и лгать. А говорит: “Я нормальный человек”.
Кто из них лжец, кто — рыцарь, а кто — нормальный человек? Ответ поясните. |
5 Февраля 2004 22:14 | |
10. |
|
6 Февраля 2004 22:32 | |
11. | Натуральное число кратно 11.
|
5 Февраля 2004 22:19 | |
12. | С одной стороны дороги росли в ряд несколько деревьев. Однажды весной между каждыми двумя соседними деревьями посадили еще по одному дереву. Следующей весной это проделали снова, а еще через год — в третий раз. Ни одно дерево за это время не погибло. Могло ли в итоге общее число деревьев стать равным 1999? |
6 Февраля 2004 23:00 | |
13. | Можно ли расставить на клетчатой доске 16 × 16 полный комплект для игры в “Морской бой” (1 кораблик 1 × 4, 2 кораблика 1 × 3, 3 кораблика 1 × 2 и 4 кораблика 1 × 1) так, чтобы в каждой вертикали и в каждой горизонтали хотя бы одна клетка была занята? |
5 Февраля 2004 22:25 | |
14. | Докажите, что квадрат нельзя разрезать на
|
6 Февраля 2004 22:34 | |
15. | Разрежьте квадрат на
|
5 Февраля 2004 22:29 | |
16. | В классе число отсутствующих учеников составляет 1/6 часть от числа присутствующих. После того, как из класса вышел один ученик, число отсутствующих стало равно 1/5 числа присутствующих. Сколько всего учеников в классе? |
5 Февраля 2004 22:29 | |
17. | Цифры семизначного числа А записали в обратном порядке и получили число В. Может ли число, равное сумме А и В, состоять только из нечетных цифр? |
5 Февраля 2004 22:30 | |
18. | Предположим, что сейчас угол между часовой и минутной стрелкой такой же, каким он был два часа назад. Чему равен этот угол? |
5 Февраля 2004 22:31 | |
19. | Найти все двузначные натуральные числа, которые в пять раз больше суммы своих цифр? |
5 Февраля 2004 22:32 | |
20. | Можно ли квадрат со стороной 20 см разрезать на 10 попарно неравных квадратов (то есть все квадраты различны), длины сторон которых выражаются целым числом сантиметров? |
5 Февраля 2004 22:33 | |
21. | Два мудреца написали на семи карточках числа от 5 до 11. После этого они перемешали карточки. Первый мудрец взял себе три карточки, второй — две, а оставшиеся они не глядя убрали в мешок. Изучив свои карточки, первый мудрец сказал второму: «Я знаю, что сумма чисел на твоих карточках четна!» а) Приведите набор чисел, которые могли быть на карточках первого мудреца. б) Докажите, что другого набора быть не может. |
5 Февраля 2004 22:33 | |
22. | Дан числовой ребус УДАР + УДАР = ДРАКА. Одинаковые буквы соответствуют одинаковым цифрам, а разные — разным. а) Найти одно решение ребуса. б) Найти все решения этого ребуса и доказать, что других решений нет. |
5 Февраля 2004 22:34 | |
23. | Дан кубик 1 × 1 × 1. Можно ли его оклеить полоской 1 × 12 в два слоя без разрывов? |
5 Февраля 2004 22:35 | |
24. | Пол в душевой комнате площадью 41 м2 устлан тремя одинаковыми коврами, каждый площадью 19 м2. Любые два ковра пересекаются по площади 7 м2. Сколько квадратных метров комнаты покрыты всеми тремя коврами? |
5 Февраля 2004 22:36 | |
25. |
|
5 Февраля 2004 22:37 | |
| Страницы: 1 | |
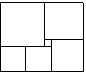 Прямоугольник на рисунке составлен
из квадратов. Найти длину стороны самого большого квадрата, если длина стороны
самого маленького равна 1.
Прямоугольник на рисунке составлен
из квадратов. Найти длину стороны самого большого квадрата, если длина стороны
самого маленького равна 1.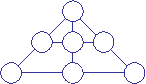 В кружочки расставляют числа
1, 2, 3, 4, 5, 6, 7 так, чтобы суммы чисел, стоящих на одной прямой, были равны
(в каждой сумме по три числа).
В кружочки расставляют числа
1, 2, 3, 4, 5, 6, 7 так, чтобы суммы чисел, стоящих на одной прямой, были равны
(в каждой сумме по три числа).