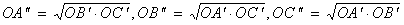358
476
всего разделов:
активных пользователей:
30 мартра 2005
Форумы снова функционируют.
21 декабря 2004
Видимо в связи с обнаруженными дырами в phpBB, форум был взломан, а через него взломано и всё остальное содержимое ceemat.ru. Всё кроме форума восстановлено, ведется дискуссия по поводу его сохранения.
Приносим извинения за неудобства.
29 сентября 2004
Форум обновился до версии 2.0.10
15 мая 2004
Новый раздел: "Программирование"
16 апреля 2004 года
Задачи Ярославского турнира математических боев — 124 задачи с решениями.
29 марта 2004
Таллинская викторина: занимательные вопросы и задачи для увлеченных химией.
6. Вписанный угол и подобные треугольники (11)
Задача 2.59 а) Стороны угла с вершиной C касаются окружности
в точках A и B. Из точки P, лежащей на окружности, опущены перпендикуляры PA1,PB1 и PC1 на прямые BC,CA
и AB. Докажите, что б) Из произвольной точки O вписанной окружности
треугольника ABC опущены перпендикуляры OAў,OBў,OCў
на стороны треугольника ABC и перпендикуляры OAўў,OBўў,OCўў
на стороны треугольника с вершинами в точках касания.
Докажите, что |
| a) б) Согласно пункту а)
|
30 Января 2004 1:00 Раздел каталога :: Ссылка на задачу
|