358
476
всего разделов:
активных пользователей:
30 мартра 2005
Форумы снова функционируют.
21 декабря 2004
Видимо в связи с обнаруженными дырами в phpBB, форум был взломан, а через него взломано и всё остальное содержимое ceemat.ru. Всё кроме форума восстановлено, ведется дискуссия по поводу его сохранения.
Приносим извинения за неудобства.
29 сентября 2004
Форум обновился до версии 2.0.10
15 мая 2004
Новый раздел: "Программирование"
16 апреля 2004 года
Задачи Ярославского турнира математических боев — 124 задачи с решениями.
29 марта 2004
Таллинская викторина: занимательные вопросы и задачи для увлеченных химией.
М761 - М780 (20)
| Страницы: 1 2 » | |
1. | M761
Докажите, что медианы АK и СL делят отрезок ЕF на три одинаковые части. |
18 Января 2004 21:31 | |
2. | M762 Докажите, что для любых положительных чисел a, b, c выполнены неравенства
|
18 Января 2004 21:32 | |
3. | M763*
Найдите отношение QA : QD, если известно отношение AC : BD = k. |
18 Января 2004 21:33 | |
4. | M764 Докажите, что каждое из уравнений а) x2 + y3 = z5; б) x2 + y3 + z5 = t7 имеет бесконечно много решений в натуральных числах. |
18 Января 2004 21:35 | |
5. | M765 Пусть B — конечное множество точек на плоскости, не принадлежащих одной прямой. а) Докажите, что найдутся три точки множества B такие, что проходящая через них окружность не содержит внутри себя других точек множества B. б)* Назовем триангуляцией множества B семейство треугольников с множеством вершин B, не налегающих друг на друга и в объединении дающих выпуклый многоугольник (триангуляцию множества B можно получить, соединяя его точки непересекающимися отрезками, пока это возможно). Докажите, что для любого B существует такая триангуляция, что окружность, описанная около любого треугольника этой триангуляции, не содержит внутри себя точек множества B. Укажите способ построения такой триангуляции. в)* Докажите, что если никакие четыре точки множества B не лежат на одной окружности, то описанная в пункте б) триангуляция единственна. |
18 Января 2004 21:35 | |
6. | M766 Докажите, что сумма квадратов трех последовательных целых чисел не может быть кубом натурального числа. |
18 Января 2004 21:36 | |
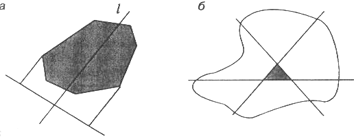
7. | M767 а) Прямая l делит площадь выпуклого многоугольника пополам.
Докажите, что отношение, в котором эта прямая делит проекцию многоугольника на
перпендикулярную к ней прямую, не превосходит
1 +
б) Каждая из трех прямых делит площадь данной фигуры пополам. Докажите, что площадь части фигуры, заключенной в треугольнике между тремя прямыми, не превосходит 1/4 всей площади фигуры (показано на рисунке б). |
18 Января 2004 21:37 | |
8. | M768* Сумма n чисел, каждое из которых не превосходит по модулю 1, равно s. Докажите, что из них можно выбрать несколько чисел так, что сумма выбранных чисел будет отличаться от s/3 не более чем на 1/3. |
18 Января 2004 21:38 | |
9. | M769*
а) б) в) |
18 Января 2004 21:39 | |
10. | M770* В основании треугольной пирамиды PABC лежит правильный треугольник АВС. Докажите, что если углы PAB, PBC, PCA равны, то пирамида PABC — правильная. |
18 Января 2004 21:40 | |
| Страницы: 1 2 » | |
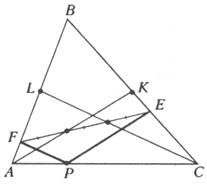 Через произвольную точку Р на стороне АС треугольника АВС
параллельно его медианам АK и СL проведены прямые, пересекающие
стороны ВС и АВ в точках Е и F соответственно (показано на рисунке).
Через произвольную точку Р на стороне АС треугольника АВС
параллельно его медианам АK и СL проведены прямые, пересекающие
стороны ВС и АВ в точках Е и F соответственно (показано на рисунке).
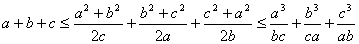
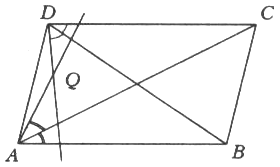 Дан параллелограмм АВСD, отличный от ромба. Прямая, симметричная
прямой АВ относительно диагонали АС, пересекает в точке Q прямую, симметричную прямой DС относительно диагонали DВ
(показано на рисунке).
Дан параллелограмм АВСD, отличный от ромба. Прямая, симметричная
прямой АВ относительно диагонали АС, пересекает в точке Q прямую, симметричную прямой DС относительно диагонали DВ
(показано на рисунке).
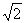 (показано на рисунке a).
(показано на рисунке a).
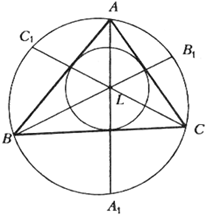 Биссектрисы треугольника АВС пересекаются в точке L, их продолжения
пересекают описанную окружность треугольника в точках
A1, B1, C1 (показано на рисунке).
Пусть R — радиус описанной, r — радиус вписанной окружности треугольника АВС.
Докажите равенства
Биссектрисы треугольника АВС пересекаются в точке L, их продолжения
пересекают описанную окружность треугольника в точках
A1, B1, C1 (показано на рисунке).
Пусть R — радиус описанной, r — радиус вписанной окружности треугольника АВС.
Докажите равенства
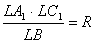 ;
;
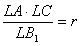 ;
;
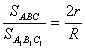 .
.