358
476
всего разделов:
активных пользователей:
30 мартра 2005
Форумы снова функционируют.
21 декабря 2004
Видимо в связи с обнаруженными дырами в phpBB, форум был взломан, а через него взломано и всё остальное содержимое ceemat.ru. Всё кроме форума восстановлено, ведется дискуссия по поводу его сохранения.
Приносим извинения за неудобства.
29 сентября 2004
Форум обновился до версии 2.0.10
15 мая 2004
Новый раздел: "Программирование"
16 апреля 2004 года
Задачи Ярославского турнира математических боев — 124 задачи с решениями.
29 марта 2004
Таллинская викторина: занимательные вопросы и задачи для увлеченных химией.
М741 - М760 (20)
| Страницы: « 1 2 3 4 » | |
6. | M746
а) полученный девятиугольник имел наибольшую площадь? б)* в нем помещалась окружность наибольшего возможного радиуса (показано на рисунке)? |
18 Января 2004 21:14 | |
7. | M747 а) Сумма n чисел равна 0, сумма их модулей равна a. Докажите, что разность между наибольшим и наименьшим из них не меньше 2a/n. б)* Внутри выпуклого n-угольника
А1A2A3...An
выбрана точка O так, что сумма векторов
в)* Можно ли улучшить эту оценку (при некоторых n)? |
18 Января 2004 21:15 | |
8. | M748
б)* В пространстве расположено несколько непересекающихся конусов. Докажите, что их нельзя переместить так, чтобы они покрыли все пространство. (Конусом мы называем здесь неограниченную выпуклую фигуру, полученную в результате вращения некоторого угла вокруг его биссектрисы.) |
18 Января 2004 21:16 | |
9. | M749* а) Докажите, что если x1, x2, x3 —
положительные числа, то б) Докажите, что если x1, x2, ..., xn —
положительные числа, то
в) Докажите, что при n > 4 неравенство пункта б) является точным в том смысле, что ни при каком n число 2 в правой части нельзя заменить на большее. |
18 Января 2004 21:17 | |
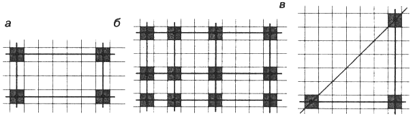
10. | M750 Докажите, что как бы ни раскрасить клетки бесконечного листа клетчатой бумаги в N цветов, найдутся а) прямоугольник, вершины которого лежат в центрах клеток одного цвета (а стороны идут параллельно линиям сетки — по горизонтальным и вертикальным прямым — см. рисунок а); б) l горизонтальных и m вертикальных прямых, которые пересекаются в центрах lm клеток одного цвета (l и m — любые натуральные числа — см. рисунок б);
в) равнобедренный прямоугольный треугольник, вершины которого — центры клеток одного цвета, при N = 2 (показано на рисунке в); г)* то же для N = 3. |
18 Января 2004 21:18 | |
| Страницы: « 1 2 3 4 » | |
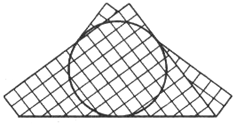 Бумажный квадрат складывается пополам по некоторой прямой l,
проходящей через его центр, в (невыпуклый) девятиугольник. Как нужно
провести прямую l, чтобы:
Бумажный квадрат складывается пополам по некоторой прямой l,
проходящей через его центр, в (невыпуклый) девятиугольник. Как нужно
провести прямую l, чтобы:
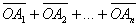 равна нулевому вектору, а сумма их длин равна d. Докажите, что периметр
этого n-угольника не меньше 4d/n.
равна нулевому вектору, а сумма их длин равна d. Докажите, что периметр
этого n-угольника не меньше 4d/n.
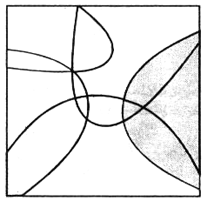 а) Можно ли разместить на плоскости конечное число парабол так, чтобы их
внутренние области покрыли всю плоскость? (Внутренней областью параболы
мы называем выпуклую фигуру, границей которой служит эта парабола — см. рисунок)
а) Можно ли разместить на плоскости конечное число парабол так, чтобы их
внутренние области покрыли всю плоскость? (Внутренней областью параболы
мы называем выпуклую фигуру, границей которой служит эта парабола — см. рисунок)
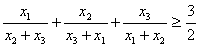 ;
;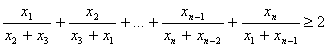 ;
;