358
473
всего разделов:
активных пользователей:
30 мартра 2005
Форумы снова функционируют.
21 декабря 2004
Видимо в связи с обнаруженными дырами в phpBB, форум был взломан, а через него взломано и всё остальное содержимое ceemat.ru. Всё кроме форума восстановлено, ведется дискуссия по поводу его сохранения.
Приносим извинения за неудобства.
29 сентября 2004
Форум обновился до версии 2.0.10
15 мая 2004
Новый раздел: "Программирование"
16 апреля 2004 года
Задачи Ярославского турнира математических боев — 124 задачи с решениями.
29 марта 2004
Таллинская викторина: занимательные вопросы и задачи для увлеченных химией.
М741 - М760 (20)
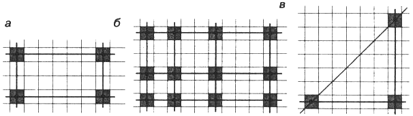
M750 Докажите, что как бы ни раскрасить клетки бесконечного листа клетчатой бумаги в N цветов, найдутся а) прямоугольник, вершины которого лежат в центрах клеток одного цвета (а стороны идут параллельно линиям сетки — по горизонтальным и вертикальным прямым — см. рисунок а); б) l горизонтальных и m вертикальных прямых, которые пересекаются в центрах lm клеток одного цвета (l и m — любые натуральные числа — см. рисунок б);
в) равнобедренный прямоугольный треугольник, вершины которого — центры клеток одного цвета, при N = 2 (показано на рисунке в); г)* то же для N = 3. |
18 Января 2004 21:18 Раздел каталога :: Ссылка на задачу
|