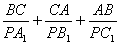358
476
всего разделов:
активных пользователей:
30 мартра 2005
Форумы снова функционируют.
21 декабря 2004
Видимо в связи с обнаруженными дырами в phpBB, форум был взломан, а через него взломано и всё остальное содержимое ceemat.ru. Всё кроме форума восстановлено, ведется дискуссия по поводу его сохранения.
Приносим извинения за неудобства.
29 сентября 2004
Форум обновился до версии 2.0.10
15 мая 2004
Новый раздел: "Программирование"
16 апреля 2004 года
Задачи Ярославского турнира математических боев — 124 задачи с решениями.
29 марта 2004
Таллинская викторина: занимательные вопросы и задачи для увлеченных химией.
M701 - M720 (20)
| Страницы: « 1 2 | |
11. | M711 Диагонали выпуклого четырехугольника ABCD, вписанного в окружность с центром О, взаимно перпендикулярны. Докажите, что ломаная АОС делит четырехугольник на две части равной площади. |
18 Января 2004 12:02 | |
12. | M712 Докажите, что любое положительное число можно представить в виде суммы девяти чисел, десятичные записи которых содержат только цифры от 0 до 7. |
18 Января 2004 12:03 | |
13. | M713 M — множество точек на плоскости. Точка O плоскости называется «почти центром симметрии» множества M, если из M можно выбросить одну точку такую, что для оставшегося множества O является центром симметрии в обычном смысле. Сколько «почти центров симметрии» может иметь конечное множество? |
18 Января 2004 12:04 | |
14. | M714* N друзей одновременно узнали N новостей, причем каждый узнал одну новость. Они стали звонить друг другу и обмениваться новостями. За один разговор можно передать сколько угодно новостей. Какое минимальное количество звонков необходимо, чтобы все узнали все новости? Рассмотрите три случая: а) N = 64; б) N = 55; в) N = 100. |
18 Января 2004 12:07 | |
15. | M715*
а) из трех,
показанные на рисунках а—в внизу?
|
18 Января 2004 14:11 | |
16. | M716 Из точки P внутри данного треугольника АВС опускаются перпендикуляры PA1, PB1, PC1 на прямые ВС, АС и АВ. Для каких точек P внутри треугольника АВС величина
|
18 Января 2004 14:01 | |
17. | M717 Даны натуральные числа
n и r, 1 £ r £ n.
Рассмотрим всевозможные подмножества множества |
18 Января 2004 14:01 | |
18. | M718 Найдите наибольшее значение выражения вида
m2 + n2 для всевозможных пар
(m; n) натуральных чисел, таких что
1 £ m £1981,
1 £ n £1981
и |
18 Января 2004 14:03 | |
19. | M719 а) Для каких n ³ З существует множество из n последовательных натуральных чисел, обладающих следующим свойством: наибольшее из этих п чисел является делителем наименьшего общего кратного остальных n - 1 чисел? б) При каких n ³ З существует единственное множество из n последовательных чисел, обладающих указанным свойством? |
18 Января 2004 14:04 | |
20. | M720 Про функцию f, определенную на множестве всех пар неотрицательных целых чисел (x; y), известно следующее: 1) f(0; y) = y + 1, 2) f(x + 1; 0) = f(x; 1), 3) f(x + 1; y + 1) = f(x; f(x + 1; y)) для каждой пары x ³ 0, y ³ 0. Найдите значение f(4; 1981). |
18 Января 2004 14:08 | |
| Страницы: « 1 2 | |
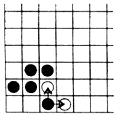 Прямой угол разбит на клетки (показано на рисунке справа). На некоторых клетках стоят фишки,
причем расположение фишек можно преобразовывать так: если для некоторой фишки
соседняя сверху и соседняя справа клетки свободны, то в эти клетки ставится по
фишке, а старая фишка убирается. Вначале в угловую клетку ставится одна фишка.
Можно ли указанными операциями освободить от фишек уголки
Прямой угол разбит на клетки (показано на рисунке справа). На некоторых клетках стоят фишки,
причем расположение фишек можно преобразовывать так: если для некоторой фишки
соседняя сверху и соседняя справа клетки свободны, то в эти клетки ставится по
фишке, а старая фишка убирается. Вначале в угловую клетку ставится одна фишка.
Можно ли указанными операциями освободить от фишек уголки