358
476
всего разделов:
активных пользователей:
30 мартра 2005
Форумы снова функционируют.
21 декабря 2004
Видимо в связи с обнаруженными дырами в phpBB, форум был взломан, а через него взломано и всё остальное содержимое ceemat.ru. Всё кроме форума восстановлено, ведется дискуссия по поводу его сохранения.
Приносим извинения за неудобства.
29 сентября 2004
Форум обновился до версии 2.0.10
15 мая 2004
Новый раздел: "Программирование"
16 апреля 2004 года
Задачи Ярославского турнира математических боев — 124 задачи с решениями.
29 марта 2004
Таллинская викторина: занимательные вопросы и задачи для увлеченных химией.
M701 - M720 (20)
| Страницы: « 1 2 3 4 » | |
6. | M706
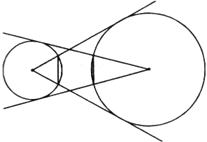
Из центра каждой из двух данных окружностей проведены касательные к другой окружности. Докажите, что хорды, соединяющие точки пересечения касательных с окружностями (показано на рисунке), имеют одинаковые длины. |
18 Января 2004 11:51 | |
7. | M707 Каждый из учеников класса занимается не более чем в двух кружках, причем для любой пары учеников существует кружок, в котором они занимаются вместе. Докажите, что найдется кружок, где занимаются не менее 2/3 учеников этого класса. |
18 Января 2004 11:52 | |
8. | M708 На сторонах выпуклого четырехугольника площадью S вне его построены квадраты, центры которых служат вершинами нового четырехугольника площадью . Докажите, что а) S1³2S; б) S1=2S в том и только в том случае, когда диагонали исходного четырехугольника равны по длине и взаимно перпендикулярны. |
18 Января 2004 11:55 | |
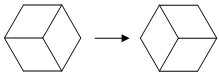
9. | M709* Пол комнаты, имеющей форму правильного шестиугольника со стороной 10, заполнен плитками, имеющими форму ромба со стороной 1 и острым углом 60°. Разрешается вынуть три плитки, составляющие правильный шестиугольник со стороной 1, и заменить их расположение другим:
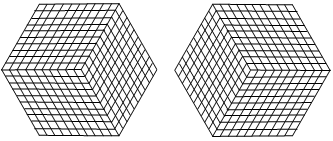
Докажите, что а) из любого расположения плиток такими операциями можно получить любое другое; б) это можно сделать не более чем за 1000 операций; в) из расположения плиток нижнего левого рисунка нельзя получить расположение рисунка нижнего правого менее чем за 1000 операций.
|
18 Января 2004 13:57 | |
10. | M710* Существует ли последовательность различных натуральных чисел a1 ,a2, a3 ,..., ни один из членов которой не равен сумме нескольких других, такая что (при всех n = 1, 2, ...) а) an £ 2 × (3)n/2; б) an £ 10 × (1,5)n; в) an £ n10; г) an £ 1000n7/2; д) an £ 1000n3/2? |
18 Января 2004 12:02 | |
| Страницы: « 1 2 3 4 » | |