358
470
всего разделов:
активных пользователей:
30 мартра 2005
Форумы снова функционируют.
21 декабря 2004
Видимо в связи с обнаруженными дырами в phpBB, форум был взломан, а через него взломано и всё остальное содержимое ceemat.ru. Всё кроме форума восстановлено, ведется дискуссия по поводу его сохранения.
Приносим извинения за неудобства.
29 сентября 2004
Форум обновился до версии 2.0.10
15 мая 2004
Новый раздел: "Программирование"
16 апреля 2004 года
Задачи Ярославского турнира математических боев — 124 задачи с решениями.
29 марта 2004
Таллинская викторина: занимательные вопросы и задачи для увлеченных химией.
10-11 класс (8)
| Страницы: 1 | |
1. | Имеется две группы по n гирь, в каждой из которых гири расположены в порядке возрастания их масс. Докажите, что 2n – 1 взвешиваниями можно расположить и все 2n гирь в порядке возрастания их масс. |
14 Января 2004 23:12 | |
2. | В треугольнике ABC сторона AB не равна другим сторонам, медианы AM и BN пересекаются в точке G, а BE и AD — биссектрисы. Докажите, что точки D, E, M и N лежат на одной окружности тогда и только тогда, когда четырехугольник CMGN — описанный. |
14 Января 2004 23:14 | |
3. | Внутри куба расположен выпуклый многогранник, проекция которого на каждую из граней куба совпадает с этой гранью. Докажите, что объем этого многогранника не меньше 1/3 объема куба. |
14 Января 2004 23:14 | |
4. | В множестве, состоящем из n элементов, выбрано 2n-1 подмножеств, каждые три из которых имеют общий элемент. Докажите, что все эти подмножества имеют общий элемент. |
14 Января 2004 23:14 | |
5. | Назовем число уравновешенным, если в его десятичной записи некоторое начало совпадает с некоторым концом (например, числа 1971, 19219 уравновешенные, а число 1415145 — нет). Докажите, что существует число, которое после приписывания к нему справа любой из десяти цифр становится уравновешенным. |
14 Января 2004 23:14 | |
6. | Пусть |
14 Января 2004 23:15 | |
7. | Несколько друзей перезванивались в новогоднюю ночь. Каждый поговорил с каждым ровно один раз. Известно, что после полуночи каждому позвонили столько же раз, сколько и до полуночи. При каком числе друзей такое возможно? |
14 Января 2004 23:15 | |
8. | Есть куча фишек разных цветов — по 100 фишек каждого цвета, и пустая шахматная доска. Играют двое. Первый выбирает фишку из кучи, второй ставит ее на свободную клетку. Если образуется ряд из 4 или более фишек подряд одного цвета, эти фишки снимаются с доски и больше в игре не участвуют. Если в куче кончились фишки, проиграл первый, если место на доске — второй. При каком наименьшем числе цветов первый может гарантированно выиграть? |
14 Января 2004 23:16 | |
| Страницы: 1 | |
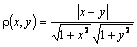 .
.