358
476
всего разделов:
активных пользователей:
30 мартра 2005
Форумы снова функционируют.
21 декабря 2004
Видимо в связи с обнаруженными дырами в phpBB, форум был взломан, а через него взломано и всё остальное содержимое ceemat.ru. Всё кроме форума восстановлено, ведется дискуссия по поводу его сохранения.
Приносим извинения за неудобства.
29 сентября 2004
Форум обновился до версии 2.0.10
15 мая 2004
Новый раздел: "Программирование"
16 апреля 2004 года
Задачи Ярославского турнира математических боев — 124 задачи с решениями.
29 марта 2004
Таллинская викторина: занимательные вопросы и задачи для увлеченных химией.
6-7 класс (8)
| Страницы: 1 | |
1. | На доске написаны все целые числа от 1 до 14. Двое играющих по очереди стирают по одному числу. Если сумма последних двух чисел — точный квадрат, то выигрывает второй, иначе — первый. Кто выигрывает при правильной игре? |
30 Января 2004 22:47 | |
2. | Петя выписал по кругу в некотором порядке целые числа от 1 до 8 и затем отметил те из них, которые равны сумме двух своих соседей. Какое наибольшее количество чисел могло быть отмечено? |
14 Января 2004 22:59 | |
3. | По углам бассейна 10м × 25м стоят Аня, Боря, Вера и Гена, а где-то у края бассейна стоит их учительница. Она позвала к себе ребят, но подошли только трое, пройдя в сумме 50 м, а к Гене учительнице пришлось идти самой. Какое расстояние прошла учительница, если все шли кратчайшим путем? |
14 Января 2004 22:59 | |
4. | Можно ли записать в строку несколько целых чисел так, чтобы среди них ровно два не делились на 2, ровно три — на 3, ровно четыре — на 4, ровно пять — на 5 и ровно шесть — на 6? |
14 Января 2004 23:00 | |
5. |
|
30 Января 2004 21:46 | |
6. | Семиклассник разрезал бумажный квадрат на прямоугольники периметра 7см, а восьмиклассник точно такой же квадрат — на прямоугольники периметра 8см. Могло ли у восьмиклассника получиться больше прямоугольников? |
14 Января 2004 23:05 | |
7. | Прямоугольник размером 204 × 2004 замощен одним слоем костяшек домино (каждая костяшка покрывает ровно две клетки). Докажите, что его можно замостить вторым слоем так, чтобы каждая плитка верхнего слоя опиралась на две разные плитки нижнего слоя. |
14 Января 2004 23:08 | |
8. | Пятнадцать друзей перезванивались в новогоднюю ночь. Каждый из них утверждает, что поговорил с каждым ровно один раз, при этом после полуночи ему позвонили столько же раз, сколько и до полуночи. Возможно ли такое? |
30 Января 2004 22:54 | |
| Страницы: 1 | |
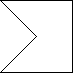 Разрежьте фигуру, изображенную на рисунке, на четыре части,
которыми можно полностью оклеить куб без наложений.
Разрежьте фигуру, изображенную на рисунке, на четыре части,
которыми можно полностью оклеить куб без наложений.