358
476
всего разделов:
активных пользователей:
30 мартра 2005
Форумы снова функционируют.
21 декабря 2004
Видимо в связи с обнаруженными дырами в phpBB, форум был взломан, а через него взломано и всё остальное содержимое ceemat.ru. Всё кроме форума восстановлено, ведется дискуссия по поводу его сохранения.
Приносим извинения за неудобства.
29 сентября 2004
Форум обновился до версии 2.0.10
15 мая 2004
Новый раздел: "Программирование"
16 апреля 2004 года
Задачи Ярославского турнира математических боев — 124 задачи с решениями.
29 марта 2004
Таллинская викторина: занимательные вопросы и задачи для увлеченных химией.
M681 - M700 (20)
| Страницы: « 1 2 3 4 » | |
6. | M686 Для любого ли числа x³1
верно равенство
|
13 Января 2004 22:02 | |
7. | M687 а) В девятиугольной пирамиде все 9 боковых ребер и все 27 диагоналей основания окрашены: некоторые — в красный цвет, остальные — в синий. Докажите, что существуют три вершины пирамиды, служащие вершинами треугольника, все стороны которого окрашены в одинаковый цвет. б) Верно ли аналогичное утверждение для восьмиугольной пирамиды? |
13 Января 2004 22:02 | |
8. | M688 Даны натуральные числа a1 ,a2, ..., an такие, что ak £ k (k = 1, 2, ..., n). Докажите, что одно из выражений a1 ± a2± a3 ± ...± an равно нулю. |
13 Января 2004 22:03 | |
9. | M689 Докажите, что из одинаковых плиток, имеющих форму равнобедренных трапеций с основаниями 3 см и высотой 1 см, нельзя составить прямоугольник. |
13 Января 2004 22:03 | |
10. | М690* а) Внутри выпуклого многоугольника с площадью S1 и периметром P1
расположен выпуклый многоугольник с площадью S2 и периметром P2.
Докажите неравенство
б) Сформулируйте и докажите аналогичное утверждение для выпуклых многогранников. |
17 Января 2004 23:21 | |
| Страницы: « 1 2 3 4 » | |
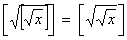 ?
? 