358
476
всего разделов:
активных пользователей:
30 мартра 2005
Форумы снова функционируют.
21 декабря 2004
Видимо в связи с обнаруженными дырами в phpBB, форум был взломан, а через него взломано и всё остальное содержимое ceemat.ru. Всё кроме форума восстановлено, ведется дискуссия по поводу его сохранения.
Приносим извинения за неудобства.
29 сентября 2004
Форум обновился до версии 2.0.10
15 мая 2004
Новый раздел: "Программирование"
16 апреля 2004 года
Задачи Ярославского турнира математических боев — 124 задачи с решениями.
29 марта 2004
Таллинская викторина: занимательные вопросы и задачи для увлеченных химией.
M681 - M700 (20)
| Страницы: 1 2 3 4 » | |
1. | M681 а) Придумайте целые числа a, b, c, d такие, что числа a2 + b2, a2 + b2+ c2, a2 + b2+ c2 + d2 — квадраты целых чисел. б) Существует ли последовательность, состоящая из квадратов целых чисел такая, что при любом n сумма n ее первых членов — квадрат целого числа? |
13 Января 2004 21:52 | |
2. | M682
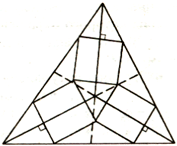
Внутри треугольника Δ нужно расположить треугольник Δ1 так, чтобы у каждого из трех квадратов, построенных на сторонах треугольника Δ1, две вершины лежали на разных сторонах треугольника Δ (показано на рисунке). а) Докажите, что медианы треугольника перпендикулярны сторонам треугольника . б) Для любого ли остроугольного треугольника такое построение возможно? |
13 Января 2004 21:56 | |
3. | M683 Несколько кружков одинакового размера положили на стол так, что никакие два не перекрываются. Докажите, что кружки можно раскрасить в четыре цвета так, что любые два касающихся кружка будут окрашены в разные цвета. Найдите расположение кружков, при котором трех цветов для такой раскраски недостаточно. |
13 Января 2004 21:58 | |
4. | M684 Двое играют в следующий вариант «морского боя». Один игрок располагает
на доске n × n некоторое количество непересекающихся «кораблей»
n × 1 (быть может, ни одного).
Второй игрок наносит одновременно ряд ударов по полям доски и
про каждое поле получает от противника ответ — попал или промахнулся. По какому
минимальному числу полей следует нанести удары, чтобы по ответу противника можно
было однозначно определить расположение всех его кораблей? Рассмотрите три случая:
|
13 Января 2004 21:59 | |
5. | M685 Два подмножества множества натуральных чисел назовем конгруэнтными, если одно получается из другого сдвигом на целое число. (Например, множество четных и нечетных чисел конгруэнтны.) Можно ли разбить множество натуральных чисел на бесконечное число (непересекающихся) бесконечных конгруэнтных подмножеств? |
13 Января 2004 22:01 | |
| Страницы: 1 2 3 4 » | |