358
476
всего разделов:
активных пользователей:
30 мартра 2005
Форумы снова функционируют.
21 декабря 2004
Видимо в связи с обнаруженными дырами в phpBB, форум был взломан, а через него взломано и всё остальное содержимое ceemat.ru. Всё кроме форума восстановлено, ведется дискуссия по поводу его сохранения.
Приносим извинения за неудобства.
29 сентября 2004
Форум обновился до версии 2.0.10
15 мая 2004
Новый раздел: "Программирование"
16 апреля 2004 года
Задачи Ярославского турнира математических боев — 124 задачи с решениями.
29 марта 2004
Таллинская викторина: занимательные вопросы и задачи для увлеченных химией.
М1861 - М1880 (20)
| Страницы: « 1 2 | |
11. | М1874 Найдите все решения уравнения ху – ух = 1 в натуральных числах х, у. |
13 Января 2004 22:13 | |
12. | М1868* Рассмотрим множество всех квадратных таблиц p × p клеток (p > 1), заполненных натуральными числами 1, 2, …, р2. Назовём правильной таблицу, в которой в первой строке (столбце) стоят по порядку числа 1, 2, …, р, во второй строке (столбце) р + 1, р + 2, …, 2р, и так далее. Пусть А — подмножество нашего множества таблиц,в котором каждую таблицу можно получить из правильной операциями перестановки столбцов и перестановки строк, В —подмножество, в котором операциями прибавления числа 1 ко всем числам строки или столбца из любой таблицы можно получить таблицу с равными числами. Докажите, что А = В тогда и только тогда, когда число р — простое. |
17 Января 2004 23:53 | |
13. | М1869 а) Решите уравнение
б) Пусть х > 0, y > 0,
x ≠ y, n, m — натуральные,
|
17 Января 2004 23:54 | |
14. | М1864
|
17 Января 2004 23:57 | |
15. | М1875 У выпуклого многогранника внутренний двугранный угол при каждом ребре острый. Сколько может быть граней у многогранника? |
13 Января 2004 22:14 | |
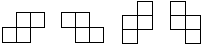
16. | М1876 а) Во всех клетках квадрата n × n стоят минусы. За один ход можно поменять знаки в одной из четырёх фигурок:
При каких n можно получить плюсы во всех клетках квадрата? б) Докажите, что если в каком-то квадрате поменяли таким образом все знаки, то при этом фигурки каждого из четырёх видов использовались одинаковое по чётности число раз. |
17 Января 2004 23:55 | |
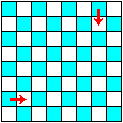
17. | М1877 За 64 хода король обошёл все поля шахматной доски и вернулся на прежнее место. Среди прочих он сделал ходы a2 — b2 и g8 — g7 (показано на рисунке).
Докажите, что король сделал не меньше двух диагональных ходов. |
18 Января 2004 0:03 | |
18. | М1878 На высоте СН треугольника АВС построена, как на диаметре, окружность. Докажите, что касательные к этой окружности, проведённые в точках её пересечения со сторонами АС и ВС, пересекаются на медиане СМ треугольника. |
13 Января 2004 22:14 | |
19. | М1879 На левую и правую чашки весов положили по 100 гирек из набора 1г, 2г, 3г, ..., 200г. Значимостью гирьки с какой-либо чашки назовём число тех гирек с другой чашки, которые легче её. Докажите, что весы покажут равновесие тогда и только тогда, когда суммарная значимость гирек левой чашки равна суммарной значимости гирек правой чашки. |
13 Января 2004 22:14 | |
20. | М1880 На прямой даны 2k - 1 белых и 2k - 1 чёрных отрезков. Известно, что любой белый отрезок пересекается хотя бы с k чёрными, а любой чёрный — хотя бы с k белыми. Докажите, что найдутся чёрный отрезок, пересекающийся со всеми белыми отрезками, и белый отрезок, пересекающийся со всеми чёрными. |
13 Января 2004 22:15 | |
| Страницы: « 1 2 | |
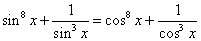 .
.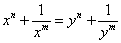 .
.
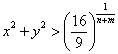 .
.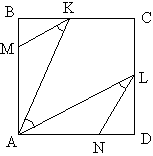 В квадрат ABCD вписана ломаная MKALN такая, что
В квадрат ABCD вписана ломаная MKALN такая, что