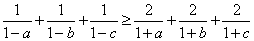358
476
всего разделов:
активных пользователей:
30 мартра 2005
Форумы снова функционируют.
21 декабря 2004
Видимо в связи с обнаруженными дырами в phpBB, форум был взломан, а через него взломано и всё остальное содержимое ceemat.ru. Всё кроме форума восстановлено, ведется дискуссия по поводу его сохранения.
Приносим извинения за неудобства.
29 сентября 2004
Форум обновился до версии 2.0.10
15 мая 2004
Новый раздел: "Программирование"
16 апреля 2004 года
Задачи Ярославского турнира математических боев — 124 задачи с решениями.
29 марта 2004
Таллинская викторина: занимательные вопросы и задачи для увлеченных химией.
М1881- (10)
| Страницы: 1 2 » | |
1. | М1881 Пусть a, b, c — положительные числа, сумма которых равна 1. Докажите неравенство
|
26 Декабря 2003 22:49 | |
2. | М1882* Изначально у Ани и Бори было по длинной полосе бумаги. На одной из них была написана буква А, а на другой Б. Каждую минуту один из них (не обязательно по очереди) приписывает к слову на своей бумажке слово с бумажки другого. Докажите, что через сутки слово с Аниной полоски можно будет разрезать на 2 части и переставить их местами так, что получится то же слово задом наперёд. |
26 Декабря 2003 22:49 | |
3. | М1883 Решите в целых числах уравнения: а) x4 - 2y2 = 1; б) x2 - 2y4 = 1; в) x4 - 8у2 = 1; г) x2 - 8y4 = 1. |
26 Декабря 2003 22:45 | |
4. | М1884 а) Квадрат разрезан на квадраты, один из которых красный, а остальные синие. Периметр каждого синего квадрата является целым числом. Докажите, что периметр красного квадрата — тоже целое число. б) Равносторонний треугольник разрезан на равносторонние треугольники, один из которых красный, а остальные синие. Периметр каждого синего треугольника является целым числом. Докажите, что периметр красного треугольника — целое число. |
26 Декабря 2003 22:45 | |
5. | М1885 Автомобильная стоянка представляет собой ряд из n мест, занумерованных слева направо числами от 1 до n, а въезд на стоянку находится справа. У въезда скопились n машин, и теперь они по очереди заезжают на стоянку. Каждый водитель сначала подъезжает к своему любимому месту. Если оно свободно, ставит туда машину, а если занято, то едет вперёд до ближайшего свободного места (назад поворачивать нельзя). Обозначим аi, где 1 £ i £ n, номер любимого места водителя i-ой в очереди машины. Будем говорить, что последовательность a1, ..., an бесконфликтна, если удаётся поставить машины на стоянку, соблюдая указанные выше правила. Например, при n = 2 последовательности (1, 2), (2, 1) и (2, 2) бесконфликтны, а последовательность (1, 1) конфликтна. а) Докажите, что последовательность натуральных чисел a1, ..., an бесконфликтна тогда и только тогда, когда ни один её член не превосходит n и когда для любого натурального k, где k < n, количество членов последовательности, не превосходящих k, не превосходит k. Найдите количество б*) бесконфликтных последовательностей длины n; в*) бесконфликтных неубывающих последовательностей длины n. |
26 Декабря 2003 22:46 | |
| Страницы: 1 2 » | |