358
471
всего разделов:
активных пользователей:
30 мартра 2005
Форумы снова функционируют.
21 декабря 2004
Видимо в связи с обнаруженными дырами в phpBB, форум был взломан, а через него взломано и всё остальное содержимое ceemat.ru. Всё кроме форума восстановлено, ведется дискуссия по поводу его сохранения.
Приносим извинения за неудобства.
29 сентября 2004
Форум обновился до версии 2.0.10
15 мая 2004
Новый раздел: "Программирование"
16 апреля 2004 года
Задачи Ярославского турнира математических боев — 124 задачи с решениями.
29 марта 2004
Таллинская викторина: занимательные вопросы и задачи для увлеченных химией.
М1881- (10)
| Страницы: « 1 2 | |
6. | М1886 На столе лежат картинками вниз 8 игральных карт. Вы можете указать на любую группу карт (в частности, на одну карту или, например, на все 8) и спросить, сколько карт бубновой масти в этой группе. В качестве ответа вам сообщат число, отличающееся от истинного значения на 1. Как при помощи 5 вопросов наверняка узнать число бубновых карт, лежащих на столе? |
29 Декабря 2003 19:01 | |
7. | М1887 Из точки пересечения диагоналей O описанного четырёхугольника ABCD опущены последовательно перпендикуляры OK, OL, OM, ON на его стороны. Докажите, что 1 / OK + 1 / OM = 1 / OL + 1 / ON. |
29 Декабря 2003 19:02 | |
8. | М1888 В шкатулке n монет достоинством в целое число дукатов каждая на сумму 2n - 1 дукатов. Доказать, что любую сумму от 1 до 2n - 1 можно предоставить монетами из шкатулки. |
29 Декабря 2003 19:03 | |
9. | М1889 На плоскости даны точки A1, A2, …, An и точки B1, B2, …, Вn. Докажите, что точки Вi можно перенумеровать так, что для всех попарно различающихся индексов i и j угол между векторами AiAj и BiBj будет острым или прямым. |
29 Декабря 2003 19:04 | |
10. | М1890
Площади восьми синих частей — рациональные числа. Докажите, что площадь красного криволинейного треугольника — рациональное число. |
29 Декабря 2003 19:16 | |
| Страницы: « 1 2 | |
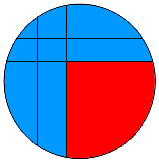Четыре хорды разделяют круг на девять частей, одна из которых является прямоугольником (показано на рисунке).