358
476
всего разделов:
активных пользователей:
30 мартра 2005
Форумы снова функционируют.
21 декабря 2004
Видимо в связи с обнаруженными дырами в phpBB, форум был взломан, а через него взломано и всё остальное содержимое ceemat.ru. Всё кроме форума восстановлено, ведется дискуссия по поводу его сохранения.
Приносим извинения за неудобства.
29 сентября 2004
Форум обновился до версии 2.0.10
15 мая 2004
Новый раздел: "Программирование"
16 апреля 2004 года
Задачи Ярославского турнира математических боев — 124 задачи с решениями.
29 марта 2004
Таллинская викторина: занимательные вопросы и задачи для увлеченных химией.
2003 год, № 5 (5)
Иллюстрации — Д. Гришуковой.
| Страницы: 1 | |
1. |
|
25 Декабря 2003 19:18 | |
2. |
|
25 Декабря 2003 19:19 | |
3. |
|
25 Декабря 2003 19:20 | |
4. |
|
25 Декабря 2003 21:36 | |
5. |
|
25 Декабря 2003 21:39 | |
| Страницы: 1 | |
 Стал я рядом с цифрой пять
Стал я рядом с цифрой пять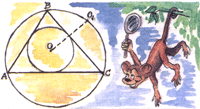 В треугольнике АВС центр вписанной окружности отразили симметрично относительно стороны
ВС — получили точку, лежащую на описанной окружности. Докажите, что угол А
равен 60°.
В треугольнике АВС центр вписанной окружности отразили симметрично относительно стороны
ВС — получили точку, лежащую на описанной окружности. Докажите, что угол А
равен 60°. На станцию Нью-Васюки прибыл товарный поезд, на каждом вагоне которого написан восьмизначный
номер. Этот номер может начинаться с нуля, но не может состоять из одних нулей. В номере
головного вагона каждая содержащаяся в нем цифра встречается одинаковое количество раз. Номер
хвостового вагона обладает таким же свойством. Какие это номера, если номер головного вагона
равен квадрату номера хвостового вагона?
На станцию Нью-Васюки прибыл товарный поезд, на каждом вагоне которого написан восьмизначный
номер. Этот номер может начинаться с нуля, но не может состоять из одних нулей. В номере
головного вагона каждая содержащаяся в нем цифра встречается одинаковое количество раз. Номер
хвостового вагона обладает таким же свойством. Какие это номера, если номер головного вагона
равен квадрату номера хвостового вагона? Профессор Мумбум-Плюмбум пытается подобрать две цифры a и b такие, что обыкновенная дробь a/b равна десятичной дроби a,b. Удастся ли ему это сделать?
Профессор Мумбум-Плюмбум пытается подобрать две цифры a и b такие, что обыкновенная дробь a/b равна десятичной дроби a,b. Удастся ли ему это сделать? Андрей взял клетчатую бумагу 10 × 10 и во всех клетках как попало провел по
одной диагонали. После чего 200 получившихся треугольников раскрасил в красный, желтый и
синий цвета так, что любые два треугольника, имеющие общую сторону, оказались окрашенными в
разные цвета. Считаете ли вы, что Андрею повезло, или трех цветов всегда достаточно?
Андрей взял клетчатую бумагу 10 × 10 и во всех клетках как попало провел по
одной диагонали. После чего 200 получившихся треугольников раскрасил в красный, желтый и
синий цвета так, что любые два треугольника, имеющие общую сторону, оказались окрашенными в
разные цвета. Считаете ли вы, что Андрею повезло, или трех цветов всегда достаточно?