358
476
всего разделов:
активных пользователей:
30 мартра 2005
Форумы снова функционируют.
21 декабря 2004
Видимо в связи с обнаруженными дырами в phpBB, форум был взломан, а через него взломано и всё остальное содержимое ceemat.ru. Всё кроме форума восстановлено, ведется дискуссия по поводу его сохранения.
Приносим извинения за неудобства.
29 сентября 2004
Форум обновился до версии 2.0.10
15 мая 2004
Новый раздел: "Программирование"
16 апреля 2004 года
Задачи Ярославского турнира математических боев — 124 задачи с решениями.
29 марта 2004
Таллинская викторина: занимательные вопросы и задачи для увлеченных химией.
2. Отношение сторон подобных треугольников (17)
Задача 1.33 Отрезок BE разбивает треугольник ABC на два подобных треугольника, причем коэффициент подобия равен |
| Так как РAEB + РBEC = 180°, то эти углы не могут быть разными углами подобных треугольников ABE и BEC, т. е. они равны и BE — перпендикуляр.
Возможны два варианта: РABE = РCBE или РABE = РBCE. Первый вариант отпадает, так как в этом случае DABE = DCBE. Остается второй вариант. В этом случае РABC = РABE + РCBE = РABE + РBAE = 90°. В прямоугольном треугольнике ABC катеты относятся, как 1 : |
17 Января 2004 15:01 Раздел каталога :: Ссылка на задачу
|
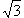 . Найдите углы треугольника ABC.
. Найдите углы треугольника ABC.