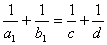358
476
всего разделов:
активных пользователей:
30 мартра 2005
Форумы снова функционируют.
21 декабря 2004
Видимо в связи с обнаруженными дырами в phpBB, форум был взломан, а через него взломано и всё остальное содержимое ceemat.ru. Всё кроме форума восстановлено, ведется дискуссия по поводу его сохранения.
Приносим извинения за неудобства.
29 сентября 2004
Форум обновился до версии 2.0.10
15 мая 2004
Новый раздел: "Программирование"
16 апреля 2004 года
Задачи Ярославского турнира математических боев — 124 задачи с решениями.
29 марта 2004
Таллинская викторина: занимательные вопросы и задачи для увлеченных химией.
1. Отрезки, заключенные между параллельными прямыми (16)
| Страницы: 1 | |
1. | Задача 1.1 Основания AD и BC трапеции ABCD равны a и b (a > b). a) Найдите длину отрезка, высекаемого диагоналями на средней линии. б) Найдите длину отрезка MN, концы которого делят стороны AB и CD в отношении AM : MB = DN : NC = p : q. |
26 Декабря 2003 22:21 | |
2. | Задача 1.2 Докажите, что середины сторон произвольного четырехугольника — вершины параллелограмма. Для каких четырехугольников этот параллелограмм является прямоугольником, для каких — ромбом, для каких — квадратом? |
31 Января 2004 15:29 | |
3. | Задача 1.3 а) Точки A1 и B1 делят стороны BC и AC треугольника ABC в отношениях б) На сторонах BC и AC треугольника ABC взяты точки A1 и B1. Отрезки AA1 и BB1 пересекаются в точке D. Пусть a1, b1, c и d - расстояния от точек A1, B1, C и D до прямой AB. Докажите, что |
27 Декабря 2003 23:22 | |
4. | Задача 1.4 Через точку P медианы CC1 треугольника ABC проведены прямые AA1 и BB1 (точки A1 и B1 лежат на сторонах BC и CA). Докажите, что A1B1 || AB. |
31 Января 2004 15:35 | |
5. | Задача 1.5 Прямая, соединяющая точку P пересечения диагоналей четырехугольника ABCD с точкой Q пересечения прямых AB и CD, делит сторону AD пополам. Докажите, что она делит пополам и сторону BC. |
27 Декабря 2003 23:25 | |
6. | Задача 1.6 На стороне AD параллелограмма ABCD взята точка P так, что AP : AD = 1 : n; Q — точка пересечения прямых AC и BP. Докажите, что AQ : AC = 1 : (n + 1). |
27 Декабря 2003 23:27 | |
7. | Задача 1.7 Вершины параллелограмма A1B1C1D1 лежат на сторонах параллелограмма ABCD (точка A1 лежит на стороне AB, точка B1 - на стороне BC и т. д.). Докажите, что центры обоих параллелограммов совпадают. |
27 Декабря 2003 23:44 | |
8. | Задача 1.8 На диагонали BD параллелограмма ABCD взята точка K. Прямая AK пересекает прямые BC и CD в точках L и M. Докажите, что AK2 = LK · KM. |
28 Января 2004 11:13 | |
9. | Задача 1.9 Одна из диагоналей вписанного в окружность четырехугольника является диаметром. Докажите, что проекции противоположных сторон на другую диагональ равны. |
30 Января 2004 23:31 | |
10. | Задача 1.10 На основании AD трапеции ABCD взята точка E так, что AE = BC. Отрезки CA и CE пересекают диагональ BD в точках O и P соответственно. Докажите, что если BO = PD, то AD2 = BC2 + AD · BC. |
27 Декабря 2003 23:50 | |
11. | Задача 1.11 Точки A и B высекают на окружности с центром O дугу величиной 60°. На этой дуге взята точка M. Докажите, что прямая, проходящая через середины отрезков MA и OB, перпендикулярна прямой, проходящей через середины отрезков MB и OA. |
28 Декабря 2003 0:33 | |
12. | Задача 1.12 а) Точки A, B и C лежат на одной прямой, а точки A1, B1, и C1 — на другой. Докажите, что если AB1||BA1 и AC1||CA1, то BC1||CB1. б) Точки A, B и C лежат на одной прямой, а точки A1, B1 и C1 таковы, что AB1||BA1, AC1||CA1 и BC1||CB1. Докажите, что точки A1, B1 и C1 лежат на одной прямой. |
28 Декабря 2003 0:37 | |
13. | Задача 1.13 В треугольнике ABC проведены биссектрисы AA1 и BB1. Докажите, что расстояние от любой точки M отрезка A1B1 до прямой AB равно сумме расстояний от M до прямых AC и BC. |
28 Декабря 2003 0:41 | |
14. | Задача 1.14 Пусть M и N — середины сторон AD и BC прямоугольника ABCD. На продолжении отрезка DC за точку D взята точка P; Q — точка пересечения прямых PM и AC. Докажите, что РQNM = РMNP. |
28 Декабря 2003 0:44 | |
15. | Задача 1.15 На продолжениях оснований AD и BC трапеции ABCD за точки A и C взяты точки K и L. Отрезок KL пересекает стороны AB и CD в точках M и N, а диагонали AC и BD в точках O и P. Докажите, что если KM = NL, то KO = PL. |
28 Декабря 2003 0:46 | |
16. | Задача 1.16 На сторонах AB, BC, CD и DA выпуклого четырехугольника ABCD взяты точки P, Q, R и S так, что BP : AB = CR : CD = a и AS : AD = BQ : BC = b. Докажите, что отрезки PR и QS делятся точкой их пересечения в отношениях b : (1 – b) и a : (1 – a). |
28 Декабря 2003 0:46 | |
| Страницы: 1 | |