358
470
всего разделов:
активных пользователей:
30 мартра 2005
Форумы снова функционируют.
21 декабря 2004
Видимо в связи с обнаруженными дырами в phpBB, форум был взломан, а через него взломано и всё остальное содержимое ceemat.ru. Всё кроме форума восстановлено, ведется дискуссия по поводу его сохранения.
Приносим извинения за неудобства.
29 сентября 2004
Форум обновился до версии 2.0.10
15 мая 2004
Новый раздел: "Программирование"
16 апреля 2004 года
Задачи Ярославского турнира математических боев — 124 задачи с решениями.
29 марта 2004
Таллинская викторина: занимательные вопросы и задачи для увлеченных химией.
Четвертый тур боев (8)
| Страницы: 1 | |
1. | В ряд выписали 101 девятку. Можно ли между ними расставить десять знаков “+” и один знак “=”, чтобы получилось верное равенство? |
21 Ноября 2003 15:39 | |
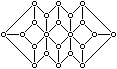
2. | Схема расположения городов и дорог в некотором государстве представлена на рисунке.
Можно ли обойти все города, побывав в каждом из них по одному разу? |
21 Ноября 2003 15:40 | |
3. | Докажите, что если значение выражения x2 – 7xy + y2 кратно 3, то оно кратно 9 (x, y — целые числа). |
21 Ноября 2003 15:41 | |
4. | Сколько существует 11-значных чисел, в записи которых встречаются все цифры? |
21 Ноября 2003 15:45 | |
5. | Числа a, b удовлетворяют равенству Найдите возможные значения выражения |
21 Ноября 2003 15:46 | |
6. | Внутри треугольника отмечены середины медиан. Докажите, что сумма расстояний от отмеченных точек до сторон треугольника меньше периметра треугольника. |
21 Ноября 2003 15:49 | |
7. |
|
21 Ноября 2003 15:52 | |
8. | Можно ли куб обклеить 12 равными квадратами, никакие два из которых не налегают друг на друга? |
21 Ноября 2003 15:52 | |
| Страницы: 1 | |
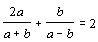 .
.
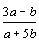 .
.
 Сад состоит из 16 одинаковых квадратных садовых участков, которыми владеют рыцари и лжецы (смотри рисунок).
Рыцари всегда говорят правду, а лжецы всегда врут. Каждый говорит, что рядом с ним живет хотя бы один рыцарь и
хотя бы один лжец (рядом — это на соседнем участке по стороне). При каком наименьшем количестве лжецов такое
может быть?
Сад состоит из 16 одинаковых квадратных садовых участков, которыми владеют рыцари и лжецы (смотри рисунок).
Рыцари всегда говорят правду, а лжецы всегда врут. Каждый говорит, что рядом с ним живет хотя бы один рыцарь и
хотя бы один лжец (рядом — это на соседнем участке по стороне). При каком наименьшем количестве лжецов такое
может быть?