358
476
всего разделов:
активных пользователей:
30 мартра 2005
Форумы снова функционируют.
21 декабря 2004
Видимо в связи с обнаруженными дырами в phpBB, форум был взломан, а через него взломано и всё остальное содержимое ceemat.ru. Всё кроме форума восстановлено, ведется дискуссия по поводу его сохранения.
Приносим извинения за неудобства.
29 сентября 2004
Форум обновился до версии 2.0.10
15 мая 2004
Новый раздел: "Программирование"
16 апреля 2004 года
Задачи Ярославского турнира математических боев — 124 задачи с решениями.
29 марта 2004
Таллинская викторина: занимательные вопросы и задачи для увлеченных химией.
Третий тур боев (14)
Квадрат со стороной 1 разрезается на прямоугольники, периметр каждого из которых равен 2.
|
Пример показан на рисунке (прямоугольники, прилегающие к сторонам квадрата, со сторонами 0,25 и 0,75, а квадрат в центре имеет стороны с длиной 0,5). b) Ответ: одним.
Аналогично, A2B = B1C, B2C = C1D, C2D = AD1. Из рисунка видно, что AD2 = A1B ³ A2B = B1C ³ B2C = C1D ³ C2D = AD1 ³ AD2. Из неравенства следует, что во всех нестрогих неравенствах должно выполняться равенство, то есть должны совпасть точки A1 и A2, B1 и B2, C1 и C2, D1 и D2. Значит, к сторонам квадрата могут примыкать только четыре равных прямоугольника (так, как в примере, приведенным в пункте a)), в центре данного квадрата они ограничивают квадрат.
c) Ответ: любое, большее трех.
Если стороны прямоугольников, прилегающих к сторонам данного квадрата, равны 1 / (2n) и (1 – 1 / (2n)), то стороны остальных прямоугольников будут равны (n – 1) / n и 1 / n. То есть периметры всех прямоугольников будут равны 2. |
Задание. Обобщим результаты задачи: можно получить любое количество частей, не меньшее 4, причем разрезать на 4, 5, 6 частей можно только единственным способом. А сколькими способами можно разрезать на n прямоугольников периметра 2 (n ³ 7)? |
21 Ноября 2003 15:06 Раздел каталога :: Ссылка на задачу
|
 a) Ответ: может.
a) Ответ: может.
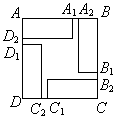 Два угла квадрата не могут принадлежать одному прямоугольнику, иначе длина одной стороны этого прямоугольника
будет равна 1, что невозможно. Значит, четыре угла квадрата занимают четыре разных прямоугольника. Так как периметр
каждого прямоугольника равен 2, то AD2 + AA1 = 1 (показано
на рисунке); но AA1 + A1B = 1,
следовательно, AD2 = A1B.
Два угла квадрата не могут принадлежать одному прямоугольнику, иначе длина одной стороны этого прямоугольника
будет равна 1, что невозможно. Значит, четыре угла квадрата занимают четыре разных прямоугольника. Так как периметр
каждого прямоугольника равен 2, то AD2 + AA1 = 1 (показано
на рисунке); но AA1 + A1B = 1,
следовательно, AD2 = A1B.
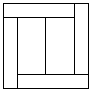 Чтобы получить 6 прямоугольников, необходимо квадрат, ограниченный прямоугольниками, разрезать на два прямоугольника.
Так как периметры прямоугольников равны, то и сами прямоугольники здесь должны быть равны. То есть, разрезать на 6 частей
можно только одним способом. Как это сделать, показано на рисунке (длины сторон прямоугольников 1 равны 1/6 и 5/6,
длины сторон прямоугольников 2 — 1/3 и 2/3).
Чтобы получить 6 прямоугольников, необходимо квадрат, ограниченный прямоугольниками, разрезать на два прямоугольника.
Так как периметры прямоугольников равны, то и сами прямоугольники здесь должны быть равны. То есть, разрезать на 6 частей
можно только одним способом. Как это сделать, показано на рисунке (длины сторон прямоугольников 1 равны 1/6 и 5/6,
длины сторон прямоугольников 2 — 1/3 и 2/3).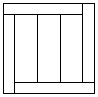 Пусть надо разрезать квадрат на (n + 3) прямоугольника периметра 2
(n ³ 1). Четыре из них будут прилегать к сторонам квадрата;
квадрат, ограниченный этими прямоугольниками разделим на n равных прямоугольников прямыми, параллельными
стороне квадрата (показано на рисунке).
Пусть надо разрезать квадрат на (n + 3) прямоугольника периметра 2
(n ³ 1). Четыре из них будут прилегать к сторонам квадрата;
квадрат, ограниченный этими прямоугольниками разделим на n равных прямоугольников прямыми, параллельными
стороне квадрата (показано на рисунке).