358
471
всего разделов:
активных пользователей:
30 мартра 2005
Форумы снова функционируют.
21 декабря 2004
Видимо в связи с обнаруженными дырами в phpBB, форум был взломан, а через него взломано и всё остальное содержимое ceemat.ru. Всё кроме форума восстановлено, ведется дискуссия по поводу его сохранения.
Приносим извинения за неудобства.
29 сентября 2004
Форум обновился до версии 2.0.10
15 мая 2004
Новый раздел: "Программирование"
16 апреля 2004 года
Задачи Ярославского турнира математических боев — 124 задачи с решениями.
29 марта 2004
Таллинская викторина: занимательные вопросы и задачи для увлеченных химией.
Второй тур боев (10)
На рисунке даны оси координат и три графика линейных функций y = a1x + b1, y = a2x + b2, y = a3x + b3 (на координатных осях заданы направления и единичные отрезки). С помощью циркуля и линейки построить отрезок длины ½a1 + a2 + a3½. |
Из выше сказанного для графиков функций y = a1x + b1, y = a2x + b2, y = a3x + b3 можно построить отрезки с длинами ½a1½, ½a2½, ½a3½, а также узнать знаки, учитывая это можно построить отрезок длины ½a1 + a2 + a3½. |
21 Ноября 2003 14:46 Раздел каталога :: Ссылка на задачу
|
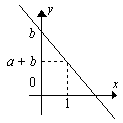Если возвести перпендикуляр к оси OX в точке с координатой 1 до пересечения с графиком функции
y = ax + b, то получим отрезок длины
½a + b½ (смотри рисунок),
причем, если точка пересечения над осью OX, то сумма a + b положительна,
если под осью OX — отрицательная. Длина отрезка от начала координат до точки пересечения графика
функции y = ax + b с осью OY равна
½b½, причем по положению точки пересечения
можно определить знак числа b. Тогда, можно построить отрезок длины
½a½
(зная длины½a + b½
и ½b½
и учитывая знаки a + b и b), а также определить знак a.