358
476
всего разделов:
активных пользователей:
30 мартра 2005
Форумы снова функционируют.
21 декабря 2004
Видимо в связи с обнаруженными дырами в phpBB, форум был взломан, а через него взломано и всё остальное содержимое ceemat.ru. Всё кроме форума восстановлено, ведется дискуссия по поводу его сохранения.
Приносим извинения за неудобства.
29 сентября 2004
Форум обновился до версии 2.0.10
15 мая 2004
Новый раздел: "Программирование"
16 апреля 2004 года
Задачи Ярославского турнира математических боев — 124 задачи с решениями.
29 марта 2004
Таллинская викторина: занимательные вопросы и задачи для увлеченных химией.
Второй тур боев (11)
| Страницы: 1 2 » | |
1. | В жилые дома стали ставить новые лифты, в которых имеется только две кнопки: при нажатии на первую лифт поднимается на 5 этажей вверх, а при нажатии на вторую – на 3 этажа вниз. (Если лифт не может выполнить одну из операций, то кнопка не срабатывает). Какое наименьшее число этажей должен иметь дом, чтобы с помощью этого лифта с любого этажа можно было попасть на любой другой? |
16 Ноября 2003 12:24 | |
2. | Гимназисты Ваня и Саша написали на доске три числа 5 и четыре числа 2. Затем Ваня перемножил некоторые из них, а Саша перемножил остальные, после чего Ваня написал на доске наибольший общий делитель этих чисел, а Саша — наименьшее общее кратное. Узнав об этом, учительница математики Вера Федоровна, не зная как ребята поделили числа и не зная, какие числа были выписаны на доску, назвала произведение выписанных НОД и НОК. Какое число назвала Вера Федоровна? |
16 Ноября 2003 12:25 | |
3. | На прямой поставили несколько точек. Затем между каждыми двумя соседними точками поставили еще по точке, и так несколько раз. Может ли после нескольких операций на прямой оказаться 1998 точек? |
16 Ноября 2003 12:25 | |
4. | Докажите, что все числа ряда 16, 1156, 111556, ... (каждое число, начиная со второго, получается вписыванием с середину числа 15) являются квадратами целых чисел. |
16 Ноября 2003 12:26 | |
5. | Братец Кролик решил сбегать к Винни-Пуху, чтобы узнать, в какое время нужно начинать праздновать Новый Год. Но вся дорога к Винни состоит только из подъемов и спусков, а Кролик на подъеме за час преодолевает 2 км, а на спуске — 3 км. Какое время затратит на дорогу туда и обратно Кролик, если от его дома до дома Пуха ровно 6 км? |
16 Ноября 2003 12:27 | |
6. |
|
16 Ноября 2003 12:27 | |
7. | Hезнайка хочет составить число так, чтобы все цифры, входящие в его запись были различны, а любые две цифры, стоящие подряд, составляли простое число. Какое наибольшее число может у него получиться? |
16 Ноября 2003 12:28 | |
8. | В ряд выписано 100 чисел. Среднее арифметическое всех без первого — 1997, всех без последнего — 1998, первого и последнего — 50,5. Каково среднее арифметическое всех чисел? |
16 Ноября 2003 12:29 | |
9. | Найти все четырехзначные числа, которые при сложении с суммой своих цифр дают пятизначное число. |
16 Ноября 2003 12:30 | |
10. |
|
16 Ноября 2003 12:30 | |
| Страницы: 1 2 » | |
 Фигуру, изображенную на рисунке нужно разрезать по сторонам квадратиков на 4 равные части так, чтобы никакие 4 квадратика, составляющие квадрат 2 ´
2 не попали в одну часть. Можно ли это сделать двумя разными способами?
Фигуру, изображенную на рисунке нужно разрезать по сторонам квадратиков на 4 равные части так, чтобы никакие 4 квадратика, составляющие квадрат 2 ´
2 не попали в одну часть. Можно ли это сделать двумя разными способами?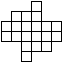 Можно ли фигуру, изображенную на рисунке разрезать по сторонам квадратиков на 4 равные части так,
чтобы никакие 4 квадратика, составляющие квадрат 2 ´ 2
не попали в одну часть?
Можно ли фигуру, изображенную на рисунке разрезать по сторонам квадратиков на 4 равные части так,
чтобы никакие 4 квадратика, составляющие квадрат 2 ´ 2
не попали в одну часть?