358
476
всего разделов:
активных пользователей:
30 мартра 2005
Форумы снова функционируют.
21 декабря 2004
Видимо в связи с обнаруженными дырами в phpBB, форум был взломан, а через него взломано и всё остальное содержимое ceemat.ru. Всё кроме форума восстановлено, ведется дискуссия по поводу его сохранения.
Приносим извинения за неудобства.
29 сентября 2004
Форум обновился до версии 2.0.10
15 мая 2004
Новый раздел: "Программирование"
16 апреля 2004 года
Задачи Ярославского турнира математических боев — 124 задачи с решениями.
29 марта 2004
Таллинская викторина: занимательные вопросы и задачи для увлеченных химией.
Вариант боев 5 (8)
Рассмотрим множество всех квадратных таблиц p ´ p клеток (p > 1), заполненных натуральными числами 1, 2, …, p2. Пусть A — подмножество, в котором каждую таблицу можно получить из правильной операциями перестановки столбцов и перестановки строк (правильная таблица — таблица, в которой в первой строке (столбце) стоят по порядку числа 1, 2, …, p, во второй строке (столбце) — p + 1, p + 2, …, 2p, и так далее); B — подмножество, в котором из любой таблицы можно получить таблицу с равными числами операциями прибавления числа 1 ко всем числам строки или столбца. Докажите, что A = B тогда и только тогда, когда p — простое. |

Решение. Будем называть операции перестановки столбцов и перестановки строк операциями типа 1, а операции прибавления числа 1 ко всем числам строки или столбца операциями типа 2. Во-первых, если число p не является простым, то подмножества A и B не совпадают. Например, при p = 4 таблица, показанная на рисунке, принадлежит множеству B, но не принадлежит множеству A. Действительно, операциями типа 2 не трудно получить таблицу с равными числами, но, переставляя столбцы или строки, нельзя получить правильную таблицу, так как при любых перестановках числа 1 и 4 будут стоят в разных строках и разных столбцах. Аналогично можно построить примеры для любого составного числа p. Во-вторых, множество A — подмножество множества B. Из правильной таблицы операциями типа 1 можно получить таблицу с равными числами. Тогда любую таблицу T из множества A можно превратить в правильную таблицу, в ней сделать все числа равными, а затем переставить столбцы и строки обратно. Это все равно, что проводить операции типа 2, так как они не зависят от расположения строк и столбцов. Значит, таблица T принадлежит множеству B. Покажем, что множество B — подмножество множества A. Назовем четверку клеток прямоугольной, если центры этих клеток являются вершинами прямоугольника со сторонами, параллельными сторонам таблицы. Для любой таблицы множества B верно следующее утверждение. 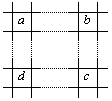
Лемма 1. Числа a, b, c и d, стоящие в этих клетках прямоугольной четверки (как на рисунке справа), удовлетворяют соотношению a + c = b + d. Для таблицы, в которой все числа равны, утверждение леммы выполнено. Применение операции, обратной операции типа 2, либо оставляет неизменными числа указанной четверки, либо уменьшает на 1 два числа в соседних вершинах прямоугольника, что также сохраняет указанное соотношение. Таким образом, для любой таблицы множества B утверждение леммы 1 верно, так как она получается из таблицы с равными числами операциями, обратными операциям типа 2. Лемма 1 доказана. Теперь докажем, что если для любой прямоугольной четверки клеток таблицы выполняется утверждение леммы 1 и число p является простым, то в ней можно переставить столбцы и строки так, что получится правильная таблица. Этим будет доказано, что любая таблица множества B принадлежит множеству A, если p — простое число, на чем решение будет завершено. Алгоритм такой перестановки следующий:
Докажем, что при этом получится правильная таблица. Число 2 будет соседним с числом 1. Действительно, иначе оно стоит в некоторой клетке, не принадлежащей ни первому столбцу, ни первой строке. Тогда клетки с числами 1 и 2 являются противоположными в некоторой прямоугольной четверке клеток. В оставшихся двух клетках должны стоять числа, сумма которых равна 3, что невозможно. В общем случае верно такое утверждение, которое доказывается аналогично. Лемма 2. Пусть известно, какими числами заполнены все клетки какого-то левого верхнего прямоугольника таблицы, n — наименьшее число, не стоящее в этом прямоугольнике. Тогда, число n стоит вне прямоугольника в первой же клетке первого столбца или первой строки. Пусть число 2 стоит во второй клетке первой строки (случай, когда оно стоит во второй клетке первого столбца, аналогичен). Покажем, что тогда в первой строке стоят числа 1, 2, 3, …, p. Пусть это не так, и после числа 1 стоит k (1 < k < p) подряд идущих чисел 1, 2, 3, …, k, а затем стоит число большее, чем число k + 1. 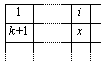
Тогда число k + 1 (согласно лемме 2) может находиться только под числом 1. Следующие k – 1 клеток второй строки определяются автоматически: это числа k + 1, k + 2, …, 2k. Действительно, любая (k + i)-я клетка второй строки (i = 2, 3, …, k) является единственной “незаполненной” клеткой какой-то прямоугольной четверки клеток (точнее, четверки с числами 1, k + 1, i), поэтому в ней стоит число x = (k + 1 + i) – 1 = k + i (показано на рисунке). Число 2k + 1 по лемме 2 стоит либо в первой строке, либо в первом столбце. Если оно стоит в первом столбце, то первые k чисел этой строки также определяются однозначно. Продолжая так определять числа, придем к тому, что найдется число вида mk + 1, которое будет стоять в (k + 1)-ой клетке первой строки. В крайнем случае, это произойдет, когда определятся все первые k клеток во всех строках. При этом будут определены все числа в верхнем левом прямоугольнике с k столбцами и m строками (в приведенном в начале примере такой блок имеет размеры 2 ´ 2). Узнав положение числа mk + 1, можно определить следующее за ним число в первой строке. Это число mk + 2. Действительно, оно либо следующее в первой строке или (m + 1)-е в первом столбце. Если оно стоит в первом столбце, то из леммы 1 следует, что число mk + k + 1 должно стоять в этой же строке в (k – 2)-ой клетке, и в то же время в клетке под числом mk + 1, что невозможно. Значит, это число стоит в следующей клетке в первой строке за числом mk + 1. Аналогично определятся следующие k – 2 числа в первой строке, а далее — следующий прямоугольник с k столбцами и m строками, заполненный числами mk + 1, mk + 2, …, 2mk. И так далее. Так можно показать, что все числа таблицы расположены блоками одинаковых размеров, каждый из которых занимает k столбцов. То есть ширина таблицы, равная числу p, должна делится на k, что невозможно (p — простое число). Значит, в первой строке стоят числа 1, 2, …, p и, исходя из выше сказанного, определяются все числа таблицы, которая оказывается правильной. Утверждение задачи доказано. |
Автор задачи — Д. Калинин Дополнение. Из решения видно, что утверждение задачи верно и для таблиц p ´ q, где p и q — простые числа. |
11 Ноября 2003 18:15 Раздел каталога :: Ссылка на задачу
|