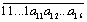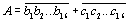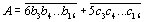358
476
всего разделов:
активных пользователей:
30 мартра 2005
Форумы снова функционируют.
21 декабря 2004
Видимо в связи с обнаруженными дырами в phpBB, форум был взломан, а через него взломано и всё остальное содержимое ceemat.ru. Всё кроме форума восстановлено, ведется дискуссия по поводу его сохранения.
Приносим извинения за неудобства.
29 сентября 2004
Форум обновился до версии 2.0.10
15 мая 2004
Новый раздел: "Программирование"
16 апреля 2004 года
Задачи Ярославского турнира математических боев — 124 задачи с решениями.
29 марта 2004
Таллинская викторина: занимательные вопросы и задачи для увлеченных химией.
Вариант боев 5 (8)
Натуральное число назовем удобным, если его можно представить в виде суммы двух натуральных слагаемых, суммы цифр которых одинаковы. Докажите, что существуют 1000000 последовательных натуральных чисел, являющихся удобными. |
Решение. Требуемым условиям удовлетворяют, например, 16-значные числа вида
где первые 10 цифр — единицы, а аi (i = 11, 12, …, 16) — любые цифры. В самом деле, если А — такое число, то либо у него, либо у числа А – 1015 сумма цифр четна, и очевидно, что при таком условии все 16 или 15 цифр разбиваются на две группы с одинаковой суммой. Обозначим эти группы через I и II. Если четной суммой цифр обладает А, то можно положить
где bi + ci = ai, i = 1, 2, …, 16, причем bi = ai, если цифра ai попала в группу I, и ci = ai, если ai попала в группу II. Если же четной суммой обладает число А – 1015, то
где bi + ci = ai, i = 3, 4, …16, причем bi = ai, если цифра ai попала в ту же группу, что и цифра a2 , и ci = ai, в противном случае. |
Автор задачи — С. Токарев |
11 Ноября 2003 18:14 Раздел каталога :: Ссылка на задачу
|