358
476
всего разделов:
активных пользователей:
30 мартра 2005
Форумы снова функционируют.
21 декабря 2004
Видимо в связи с обнаруженными дырами в phpBB, форум был взломан, а через него взломано и всё остальное содержимое ceemat.ru. Всё кроме форума восстановлено, ведется дискуссия по поводу его сохранения.
Приносим извинения за неудобства.
29 сентября 2004
Форум обновился до версии 2.0.10
15 мая 2004
Новый раздел: "Программирование"
16 апреля 2004 года
Задачи Ярославского турнира математических боев — 124 задачи с решениями.
29 марта 2004
Таллинская викторина: занимательные вопросы и задачи для увлеченных химией.
Вариант боев 5 (8)
Докажите, что ни при каких целых a, b и c числа
не могут быть целыми одновременно. |
Решение. Приведем к общему знаменателю все три выражения и получим:
Произведение этих выражений равно 1, значит, все они могут быть целыми только в том случае, если каждое из них равно 1 или –1. Если все три выражения равны 1, то
Из условия задачи следует, что abc ¹ 0, значит, (a – b)(b – c)(c – a) ¹ 0. Однако, разделив первое уравнение системы на второе, получим a : с = a2 : c2, откуда a = c. Противоречие. Если два выражения равны –1 (например, первое и второе), а третье равно 1, то
Здесь из первого уравнения следует, что c3 + (ca)b = 2ac × c, и с учетом третьего уравнения имеем c3 + b3 = 2b2c. Тогда c3 + b3 – 2b2c = c3 – b3 + 2b3 – 2b2c = (с – b)(c2 + cb + b2) + 2b2(b – c) = = (c – b)(c2 + cb – b2) = 0. Поскольку b ¹ c и b ¹ 0, то c2 + cb – b2 = 0, откуда
Значит, число c/b — корень уравнения t2 + t – 1 = 0. Но корни этого уравнения иррациональны — противоречие. |
Автор задачи — В. Каскевич |
11 Ноября 2003 18:12 Раздел каталога :: Ссылка на задачу
|
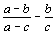 ,
, 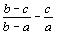 ,
, 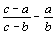
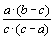 ,
, 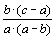 ,
, 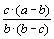 .
.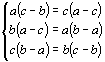 Û
Û 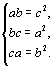
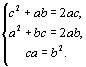
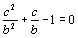 .
.