358
476
всего разделов:
активных пользователей:
30 мартра 2005
Форумы снова функционируют.
21 декабря 2004
Видимо в связи с обнаруженными дырами в phpBB, форум был взломан, а через него взломано и всё остальное содержимое ceemat.ru. Всё кроме форума восстановлено, ведется дискуссия по поводу его сохранения.
Приносим извинения за неудобства.
29 сентября 2004
Форум обновился до версии 2.0.10
15 мая 2004
Новый раздел: "Программирование"
16 апреля 2004 года
Задачи Ярославского турнира математических боев — 124 задачи с решениями.
29 марта 2004
Таллинская викторина: занимательные вопросы и задачи для увлеченных химией.
Вариант боев 5 (8)
На территории завода четыре асфальтовые дорожки длиной 10 м каждая образуют квадрат. В двух соседних вершинах квадрата стоят двое рабочих, держа на плечах десятиметровую трубу. Им необходимо, передвигаясь по дорожкам и не выпуская при этом трубы, поменяться местами. Из соображений безопасности разрешается идти со скоростью не больше 1 м/с. За какое наименьшее время рабочие могут справиться с заданием? (Внутри квадрата нет никаких сооружений, создающих помехи при переноске трубы). |
Решение. Очевидно, что если путь имеет минимальную длину, то недопустимо, чтобы в процессе движения рабочие разворачивались и шли обратно по тем же путям (если хотя бы один из них пойдет в другом направлении, то это допустимо). Заметим, что если один из рабочих в какой-то момент не находится в вершине квадрата, то второй рабочий также не находится в вершине, а на одной из трех остальных сторон квадрата. При этом движение любого из них в ту или другую сторону от своего местонахождения вызывает жестко связанное с этим (посредством трубы) движение напарника также в одну или другую сторону. Присвоим рабочим номера — первый и второй. Пусть сначала в квадрате ABCD первый рабочий находится в вершине A, а второй — в вершине В. C самого начала движения хотя бы одному из рабочих придется выйти за пределы отрезка АВ. Пусть, для определенности, это первый рабочий. Тогда он пойдет по отрезку AD к точке D. Второму рабочему можно при этом выбрать два пути от своей стартовой точки B: либо идти параллельно первому к точке C, либо перпендикулярно ему к точке А. Обозначим первую схему движения так: (1-AD, 2-BC), а вторую — так: (1- AD, 2-BA). Рассмотрим первую схему. Если первый теперь пойдет из точки D обратно в точку A, то второму на выбор есть две возможности: возвращаться в точку B или идти к точке D. Первая из них недопустима — это возврат к стартовой позиции, поэтому допустим лишь второй путь, то есть (1-ADA, 2-BCD). Далее виден наикратчайший способ выполнения поставленной задачи (поменяться местами): первый идет к точке B, второй — к точке A, и итоговая схема движения такова: (1-ADAB, 2-BCDA). Рассмотрим теперь вторую схему (1-AD, 2-BA). Если первый теперь пойдет из точки D обратно в точку A, то второму придется возвращаться в стартовую точку — это напрасная трата времени. Поэтому первый должен идти к точке С, а второму на выбор дается две возможности: идти к точке В или к точке D. Таким образом, возможный путь раздвоился: (1-ADC, 2-BAB) или (1-ADC, 2-BAD). Для каждого из этих путей, как видно, просматривается последний шаг, чтобы поменяться местами, и получаются, таким образом, маршруты: (1-ADCB, 2-BABA) или (1-ADCB, 2-BADA). Обнаружено три различных кратчайших маршрута, во всех трех каждому рабочему придется пройти по трем отрезкам, то есть длина пути каждого составит 30 м. Заметим, что если рабочие движутся не параллельно, а по двум смежным сторонам квадрата, то они не смогут одновременно выдерживать максимальную скорость 1 м/с — одному придется двигаться медленней. Рассмотрим движение одного из рабочих относительно другого в произвольный момент времени. Относительная скорость их движения есть разность векторов их скоростей. Так как расстояние между ними постоянно, то рабочие не могут удаляться или сближаться, вследствие чего проекция этой разности на направление трубы должна равняться нулю. Из этого следует, что проекции скоростей рабочих на трубу равны. Тогда быстрее идет тот рабочий, у которого угол между направлением движения и трубой больше. Именно он движется с максимальной скоростью 1 м/с, а второму приходится идти медленней. Найдем затраченное рабочими время. Все определенные выше маршруты, составлены из трех частей, одна из которых — движение по параллельным сторонам квадрата длиной 10 м (на что потрачено ровно 10 секунд), а две другие — одинаковы, и представляют собой движение по смежным взаимно перпендикулярным сторонам квадрата. Определим, сколько времени тратится на одну из частей. Первоначально первый рабочий начинает движение перпендикулярно
трубе, а второй — вдоль трубы, то есть скорость первого равна 1 м/с, а второго — нулевая. Затем постепенно
угол между трубой и скоростью первого растет, а скоростью второго — убывает, пока они оба не достигнут
45°. Путь, пройденный первым, к тому времени будет равен катету прямоугольного
равнобедренного треугольника с гипотенузой 10 м, то есть На выполнение всей задачи понадобиться Покажем, что на путь, который длиннее 30 метров, уйдет не меньше найденного выше времени. Если путь кого-то из рабочих проходит более чем по трем сторонам квадрата, то это значит, что он не короче четырех длин сторон, то есть 40 м, и даже при постоянной максимальной скорости движения (1 м/с) на все движение он затратит не менее 40 секунд, что более 38 секунд. |
Автор задачи — И. Акулич Дополнение. Еще сильнее этот эффект проявится при переноске трубы по периметру правильного треугольника. Здесь кроме рассмотренного эффекта взаимного торможения появится другой эффект: местами одному из рабочих придется пятиться назад. Но в этом случае поменяться местами невозможно, но пройтись с трубой по кругу будет непросто. Лишь окружность позволит обойти весь периметр с постоянными скоростями обоих концов. |
11 Ноября 2003 18:10 Раздел каталога :: Ссылка на задачу
|
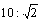 .
В этот момент скорости рабочих сравняются. Далее второй рабочий идет со скоростью 1 м/с (первый — медленней),
и пройти ему придется с этой скоростью те же
.
В этот момент скорости рабочих сравняются. Далее второй рабочий идет со скоростью 1 м/с (первый — медленней),
и пройти ему придется с этой скоростью те же 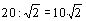 секунд.
секунд. 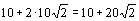 секунд (это около 38 секунд).
секунд (это около 38 секунд).