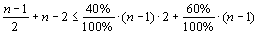358
471
всего разделов:
активных пользователей:
30 мартра 2005
Форумы снова функционируют.
21 декабря 2004
Видимо в связи с обнаруженными дырами в phpBB, форум был взломан, а через него взломано и всё остальное содержимое ceemat.ru. Всё кроме форума восстановлено, ведется дискуссия по поводу его сохранения.
Приносим извинения за неудобства.
29 сентября 2004
Форум обновился до версии 2.0.10
15 мая 2004
Новый раздел: "Программирование"
16 апреля 2004 года
Задачи Ярославского турнира математических боев — 124 задачи с решениями.
29 марта 2004
Таллинская викторина: занимательные вопросы и задачи для увлеченных химией.
Вариант боев 4 (10)
Задачи 32-39 составили боле сложный вариант, задачи 32, 33, 35, 37-41 составили менее сложный вариант
В однокруговом хоккейном турнире все команды набрали разное число очков. (В хоккее за победу дается 2 очка, за ничью 1 очко и за поражение 0 очков.) Оказалось, что команда, занявшая последнее место, выиграла не менее 25% своих матчей, а команда, занявшая второе место, выиграла не более 40% своих матчей. Какое наибольшее количество команд могло участвовать в этом турнире? |
Ответ: 9. Решение. Пусть в турнире участвовало n команд. Тогда команда, занявшая последнее место, которая выиграла не менее 25% своих матчей, набрала не менее
Все команды набрали разное число очков. Значит, команда, занявшая предпоследнее место, получила не менее (n – 1) : 2 + 1 очков, третье место с конца — не менее (n – 1) :2 + 2 очков, и так далее, команда, занявшая второе место — не менее (n – 1) : 2 + n – 2 очков, а победитель турнира — не менее (n – 1) : 2 + n – 1 очков. Тем самым, все команды вместе набрали не менее
очков. Но так как в каждом матче разыгрывалось ровно 2 очка, а число матчей равно n(n – 1) : 2, то число всех разыгранных очков также равно n(n – 1). Поэтому все ранее полученные оценки числа набранных командами очков являются точными. То есть последняя команда набрала ровно (n – 1) : 2 очков, предпоследняя — ровно (n – 1) : 2 + 1 очков, … команда, занявшая второе место — ровно (n – 1) : 2 + n – 2 очков, а победитель — ровно (n – 1) : 2 + n – 2 очков. Так как команда, занявшая второе место, выиграла не более 40% своих матчей, то
откуда после упрощения получаем, что n < 11. Учитывая, что, команда, занявшая последнее место, выиграла ровно (n – 1) : 4 матчей, число (n – 1) делится на 4. Поэтому максимально возможное значение n равно 9. Следующая таблица показывает, что такой турнир с участием 9 команд действительно мог состояться. |
Автор задачи — И. Воронович |
11 Ноября 2003 18:04 Раздел каталога :: Ссылка на задачу
|
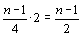очков.
