358
476
всего разделов:
активных пользователей:
30 мартра 2005
Форумы снова функционируют.
21 декабря 2004
Видимо в связи с обнаруженными дырами в phpBB, форум был взломан, а через него взломано и всё остальное содержимое ceemat.ru. Всё кроме форума восстановлено, ведется дискуссия по поводу его сохранения.
Приносим извинения за неудобства.
29 сентября 2004
Форум обновился до версии 2.0.10
15 мая 2004
Новый раздел: "Программирование"
16 апреля 2004 года
Задачи Ярославского турнира математических боев — 124 задачи с решениями.
29 марта 2004
Таллинская викторина: занимательные вопросы и задачи для увлеченных химией.
Вариант боев 2 (8)
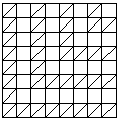
В некоторых клетках шахматной доски проведена одна из двух возможных диагоналей так, что ни для каких двух диагоналей концы их не совпадают. Какое наибольшее количество диагоналей можно провести, соблюдая такое условие? |
Ответ: 36. Решение. Отметим на доске все точки, которые могут являться концами диагоналей (очевидно, это — множество углов всех клеток доски). Всего таких точек, как легко подсчитать, 81, и образуют они квадрат из точек 9 ´ 9 — то есть 9 вертикальных рядов по 9 точек каждый. А теперь пронумеруем эти ряды слева направо числами от 1 до 9 и раскрасим точки в два цвета следующим образом: все точки рядов с нечетными номерами — в красный цвет, с четными номерами — в синий цвет. Всего получится 9 × 5 = 45 красных и 9 × 4 = 36 синих точек. Заметим, что у каждой проведенной диагонали один конец попадает в красную точку, второй — в синюю. Поэтому число диагоналей не превосходит числа синих точек, то есть 36. С другой стороны, ровно 36 диагоналей провести можно (показано на рисунке).
|
Автор задачи — И. Акулич |
10 Ноября 2003 22:11 Раздел каталога :: Ссылка на задачу
|