358
476
всего разделов:
активных пользователей:
30 мартра 2005
Форумы снова функционируют.
21 декабря 2004
Видимо в связи с обнаруженными дырами в phpBB, форум был взломан, а через него взломано и всё остальное содержимое ceemat.ru. Всё кроме форума восстановлено, ведется дискуссия по поводу его сохранения.
Приносим извинения за неудобства.
29 сентября 2004
Форум обновился до версии 2.0.10
15 мая 2004
Новый раздел: "Программирование"
16 апреля 2004 года
Задачи Ярославского турнира математических боев — 124 задачи с решениями.
29 марта 2004
Таллинская викторина: занимательные вопросы и задачи для увлеченных химией.
Вариант боев 1 (8)
Сторона BC треугольника ABC разбита точками M и N на три равные части (BM = MN = NC); K и L — середины сторон AB и AC соответственно. Прямая LM пересекает прямую AB в точке E, прямая KN пересекает прямую AC в точке F. Докажите, что прямая EF параллельна прямой BC. |
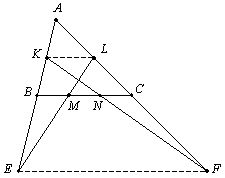
Решение 1. Рассмотрим треугольник AEC (показано на рисунке). В нем EL — медиана, которая делит отрезок CB в отношении 2:1, то есть BC — также медиана. (Действительно, если бы отрезок BC не был медианой, то прямая EL должна быть параллельная прямой AE). То есть точка B — середина отрезка AE. Аналогично доказывается, что точка C — середина стороны AF. Значит, BC — средняя линия треугольника AEF, то есть прямые BC и EF параллельны. Решение 2. Отрезок KL — средняя линия треугольника ABC, поэтому прямые KL и BC параллельны, откуда следует, что треугольники KLF и NFC — подобны. Коэффициент подобия равен KL:CN = 3:2. Из этого следует, что точка F втрое дальше от прямой KL, нежели точка C. Аналогично доказывается, что точка E втрое дальше от прямой KL, нежели точка B. Но точки B и C равноудалены от прямой KL, значит, точки E и F также равноудалены от прямой KL. То есть прямые EF и KL параллельны, откуда следует и параллельность прямых BC и EF. |
Автор задачи — Д. Калинин, г. Кострома |
10 Ноября 2003 22:02 Раздел каталога :: Ссылка на задачу
|