358
476
всего разделов:
активных пользователей:
30 мартра 2005
Форумы снова функционируют.
21 декабря 2004
Видимо в связи с обнаруженными дырами в phpBB, форум был взломан, а через него взломано и всё остальное содержимое ceemat.ru. Всё кроме форума восстановлено, ведется дискуссия по поводу его сохранения.
Приносим извинения за неудобства.
29 сентября 2004
Форум обновился до версии 2.0.10
15 мая 2004
Новый раздел: "Программирование"
16 апреля 2004 года
Задачи Ярославского турнира математических боев — 124 задачи с решениями.
29 марта 2004
Таллинская викторина: занимательные вопросы и задачи для увлеченных химией.
Вариант боев 1 (8)
В выпуклом четырехугольнике проведены биссектрисы всех его углов. Может ли каждая из сторон четырехугольника пересекаться какой-либо биссектрисой в точке, отличной от вершины? |
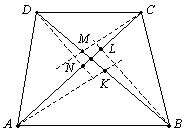
Ответ: нет. Решение. Допустим, что для некоторого четырехугольника ABCD ситуация, указанная в условии, реализуется. Пусть биссектриса угла A пересекает сторону BC (случай, когда она пересекает сторону CD аналогичен). Тогда сторону СD пересекает биссектриса угла B, сторону AD — биссектриса угла C, сторону AB — биссектриса угла D. То есть биссектрисы углов A, В, С, D пересекают отрезки ОВ, ОС, OD, ОА соответственно (пусть K, L, M, N — соответственные точки пересечения как показано на рисунке). По теореме о биссектрисе угла треугольника имеем
Легко видеть, что произведение левых частей этих равенств равно 1, в то время как
Противоречие. |
Автор задачи — И. Григорьева, г. Казань |
10 Ноября 2003 22:01 Раздел каталога :: Ссылка на задачу
|
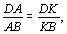
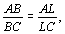
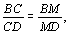
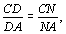
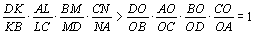 .
.