358
476
всего разделов:
активных пользователей:
30 мартра 2005
Форумы снова функционируют.
21 декабря 2004
Видимо в связи с обнаруженными дырами в phpBB, форум был взломан, а через него взломано и всё остальное содержимое ceemat.ru. Всё кроме форума восстановлено, ведется дискуссия по поводу его сохранения.
Приносим извинения за неудобства.
29 сентября 2004
Форум обновился до версии 2.0.10
15 мая 2004
Новый раздел: "Программирование"
16 апреля 2004 года
Задачи Ярославского турнира математических боев — 124 задачи с решениями.
29 марта 2004
Таллинская викторина: занимательные вопросы и задачи для увлеченных химией.
Бой за III место (8)
г.Рыбинск(2) - Гимназия(г.Ростов) (18 марта 2001 г.)
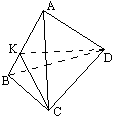
В тетраэдре ABCD угол BAC равен углу ACD, а угол ABD равен углу BDC. Докажите, что AB = CD. |
Предположим противное: AB ¹ CD. Без ограничения общности можно считать, что AB > CD. Отложим на AB отрезок AK, равный CD. Пусть ÐKDB = a. Так как AK = CD, AC — общая сторона, ÐKAC = ÐACD, то треугольники KAC и DCA равны, значит KC = AD. Тогда треугольники KDC и KDA равны (по трем сторонам), поэтому ÐAKD = ÐKDC. Так как ÐAKD = ÐABD + a (внешний угол), то ÐKDC = ÐAKD = ÐABD + a = ÐBDC + a. Тогда BD лежит в плоскости KDC, отсюда точка K совпадает с точкой B — противоречие. |
16 Апреля 2004 21:40 Раздел каталога :: Ссылка на задачу
|