358
476
всего разделов:
активных пользователей:
30 мартра 2005
Форумы снова функционируют.
21 декабря 2004
Видимо в связи с обнаруженными дырами в phpBB, форум был взломан, а через него взломано и всё остальное содержимое ceemat.ru. Всё кроме форума восстановлено, ведется дискуссия по поводу его сохранения.
Приносим извинения за неудобства.
29 сентября 2004
Форум обновился до версии 2.0.10
15 мая 2004
Новый раздел: "Программирование"
16 апреля 2004 года
Задачи Ярославского турнира математических боев — 124 задачи с решениями.
29 марта 2004
Таллинская викторина: занимательные вопросы и задачи для увлеченных химией.
Бой за III место (8)
г.Рыбинск(2) - Гимназия(г.Ростов) (18 марта 2001 г.)
На клетчатой доске размером 1000 ´ 1000 стоят красные, синие и зеленые фишки (в каждой клетке — не больше одной фишки). Рядом (в соседних по стороне клетках) с любой красной фишкой стоят 2 синие, а рядом с любой синей — 3 зеленые. Докажите, что есть зеленая фишка, рядом с которой нет красных. |
Предположим противное: у любой зеленой фишки есть соседняя красная.
|
16 Апреля 2004 21:39 Раздел каталога :: Ссылка на задачу
|
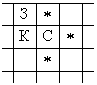 С краю не может стоять красная фишка. Действительно, если красная фишка на краю, то на краю рядом с ней должна быть синяя фишка, но тогда у этой синей фишки не может быть трех зеленых соседних фишек. То есть на краю могут быть только синие и зеленые фишки. Пусть это верхний край. Рассмотрим самую левую фишку. Не трудно доказать, что она обязана быть зеленой. По предположению рядом стоит красная фишка, она может стоять только под зеленой (не на краю). С красной граничат две синие. Одна из них должна быть слева от красной или справа. Слева от красной фишки синяя быть не может, иначе три одна из трех соседних с ней зеленых фишек должна стоять над ней на краю, а значит мы рассматривали не самую левую зеленую фишку. Значит справа от красной фишки стоит синяя (см. рисунок). Тогда в клетках, обозначенных звездочками, стоят зеленые фишки. Тогда в клетке над синей фишкой стоит зеленая фишка, не имеющая соседней красной — противоречие.
С краю не может стоять красная фишка. Действительно, если красная фишка на краю, то на краю рядом с ней должна быть синяя фишка, но тогда у этой синей фишки не может быть трех зеленых соседних фишек. То есть на краю могут быть только синие и зеленые фишки. Пусть это верхний край. Рассмотрим самую левую фишку. Не трудно доказать, что она обязана быть зеленой. По предположению рядом стоит красная фишка, она может стоять только под зеленой (не на краю). С красной граничат две синие. Одна из них должна быть слева от красной или справа. Слева от красной фишки синяя быть не может, иначе три одна из трех соседних с ней зеленых фишек должна стоять над ней на краю, а значит мы рассматривали не самую левую зеленую фишку. Значит справа от красной фишки стоит синяя (см. рисунок). Тогда в клетках, обозначенных звездочками, стоят зеленые фишки. Тогда в клетке над синей фишкой стоит зеленая фишка, не имеющая соседней красной — противоречие.