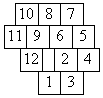358
476
всего разделов:
активных пользователей:
30 мартра 2005
Форумы снова функционируют.
21 декабря 2004
Видимо в связи с обнаруженными дырами в phpBB, форум был взломан, а через него взломано и всё остальное содержимое ceemat.ru. Всё кроме форума восстановлено, ведется дискуссия по поводу его сохранения.
Приносим извинения за неудобства.
29 сентября 2004
Форум обновился до версии 2.0.10
15 мая 2004
Новый раздел: "Программирование"
16 апреля 2004 года
Задачи Ярославского турнира математических боев — 124 задачи с решениями.
29 марта 2004
Таллинская викторина: занимательные вопросы и задачи для увлеченных химией.
Бой за III место (8)
г.Рыбинск(2) - Гимназия(г.Ростов) (18 марта 2001 г.)
Государство состоит из нескольких республик, имеющих территории в виде одинаковых квадратов. В какое наименьшее количество цветов гарантированно можно окрасить карту государства, чтобы республики с общим участком границы были окрашены в разные цвета? |
Ответ: 4 цвета. В четыре цвета такую карту покрасить можно. Идея решения: красим "построчно сверху вниз" (построчно — смещаем параллельно некоторую прямую сверху вниз; встречая неокрашенные клетки, называем их новым уровнем), каждый уровень слева направо красим в любой незапрещенный цвет. Несложно доказать, что можно выбрать цвет для покраски очередного квадрата (его соседи либо не окрашены, либо их не более 3). Теперь приведем пример, когда трех цветов недостаточно. Легко видеть, что такую
Для определенности считаем, что красим в синие, зеленые и красные цвета. Пусть клетка 1 красная, 2 — синяя. Тогда 3 должна быть зеленая, 4 — красная, 5 — зеленая, 6 — красная, 7 — синяя, 8 — зеленая, 9 — синяя, 10 — красная, 11 — зеленая; теперь получили, что клетку 12 нельзя покрасить ни в один из имеющихся цветов. Значит трех цветов недостаточно для покраски. |
16 Апреля 2004 21:38 Раздел каталога :: Ссылка на задачу
|