358
476
всего разделов:
активных пользователей:
30 мартра 2005
Форумы снова функционируют.
21 декабря 2004
Видимо в связи с обнаруженными дырами в phpBB, форум был взломан, а через него взломано и всё остальное содержимое ceemat.ru. Всё кроме форума восстановлено, ведется дискуссия по поводу его сохранения.
Приносим извинения за неудобства.
29 сентября 2004
Форум обновился до версии 2.0.10
15 мая 2004
Новый раздел: "Программирование"
16 апреля 2004 года
Задачи Ярославского турнира математических боев — 124 задачи с решениями.
29 марта 2004
Таллинская викторина: занимательные вопросы и задачи для увлеченных химией.
1/2 финала. Вариант 2 (10)
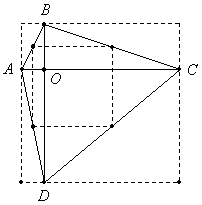
В квадрат вписан четырехугольник P (на каждой стороне квадрата по одной вершине четырехугольника), в который в свою очередь вписали квадрат (также на каждой стороне четырехугольника по одной вершине квадрата), причем все 12 вершин этих четырехугольников различны. Могло ли так получиться, что у четырехугольника P все стороны попарно различны? |
Ответ: могло. Возьмем в качестве P четырехугольник ABCD с перпендикулярными диагоналями AC и BD, причем AC = BD = 7, точка O —их пересечение; AO = 1, BO = 2, CO = 6, DO = 5.
Очевидно, что длины всех сторон ABCD различны. Возьмем середины сторон четырехугольника ABCD и последовательно их соединим. Так как каждая из сторон является средней линией треугольника, у которого основание — одна из диагоналей ABCD, то из равенства диагоналей следует равенство сторон вписанного четырехугольника. Также легко показать, что полученный вписанный четырехугольник является квадратом. |
16 Апреля 2004 21:36 Раздел каталога :: Ссылка на задачу
|