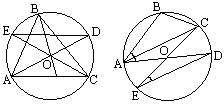358
476
всего разделов:
активных пользователей:
30 мартра 2005
Форумы снова функционируют.
21 декабря 2004
Видимо в связи с обнаруженными дырами в phpBB, форум был взломан, а через него взломано и всё остальное содержимое ceemat.ru. Всё кроме форума восстановлено, ведется дискуссия по поводу его сохранения.
Приносим извинения за неудобства.
29 сентября 2004
Форум обновился до версии 2.0.10
15 мая 2004
Новый раздел: "Программирование"
16 апреля 2004 года
Задачи Ярославского турнира математических боев — 124 задачи с решениями.
29 марта 2004
Таллинская викторина: занимательные вопросы и задачи для увлеченных химией.
1/2 финала. Вариант 1 (8)
Школа №33(1) - г.Рыбинск(2) (4 марта 2001 года)
Точка O — центр описанной окружности треугольника ABC; лучи AO и CO вторично пересекают описанную окружность соответственно в точках D и E таких, что ÐDEC = ÐDAB и ÐEDA = ÐECB. Докажите, что треугольник ABC равносторонний. |
Первый случай: центр окружности лежит внутри треугольника (треугольник остроугольный). Углы DAC и DEC равны как опирающиеся на одну дугу, из условия ÐDEC = ÐDAB, значит ÐDAC = ÐDAB. Аналогично ÐECB = ÐECA. Значит, в треугольнике ABC совпадают центры вписанной и описанной окружности. Не трудно доказать, что это возможно только в равностороннем треугольнике. Второй случай: когда центр окружности лежит вне треугольника ABC. Такое невозможно, так как из равенства углов DEC и DAB легко вывести равенство дуг BD и CD, но тогда часть дуги равна целой дуге. |
16 Апреля 2004 21:36 Раздел каталога :: Ссылка на задачу
|