358
471
всего разделов:
активных пользователей:
30 мартра 2005
Форумы снова функционируют.
21 декабря 2004
Видимо в связи с обнаруженными дырами в phpBB, форум был взломан, а через него взломано и всё остальное содержимое ceemat.ru. Всё кроме форума восстановлено, ведется дискуссия по поводу его сохранения.
Приносим извинения за неудобства.
29 сентября 2004
Форум обновился до версии 2.0.10
15 мая 2004
Новый раздел: "Программирование"
16 апреля 2004 года
Задачи Ярославского турнира математических боев — 124 задачи с решениями.
29 марта 2004
Таллинская викторина: занимательные вопросы и задачи для увлеченных химией.
1/2 финала. Вариант 1 (8)
Школа №33(1) - г.Рыбинск(2) (4 марта 2001 года)
Докажите, что сумма квадратов всех делителей натурального числа n (включая 1 и n) не может равняться (n + 1)2. |
Если n — простое число, то сумма квадратов делителей равна 1 + n2, что менее чем (n + 1)2. Если n — квадрат простого числа, то сумма квадратов делителей равна 1 + n2 + n, что также менее чем (n + 1)2. Если не выполнены первые два условия, то у числа n есть делитель k, отличный от 1, n и |
16 Апреля 2004 21:34 Раздел каталога :: Ссылка на задачу
|
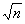. Тогда сумма квадратов делителей не менее чем 1 + n2 + k2 + (n / k)2. По неравенству Коши k2 + (n / k)2 > 2n (так как k ¹ n / k). Тогда 1 + n2 + k2 + (n / k)2 > (n + 1)2.