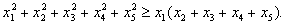358
476
всего разделов:
активных пользователей:
30 мартра 2005
Форумы снова функционируют.
21 декабря 2004
Видимо в связи с обнаруженными дырами в phpBB, форум был взломан, а через него взломано и всё остальное содержимое ceemat.ru. Всё кроме форума восстановлено, ведется дискуссия по поводу его сохранения.
Приносим извинения за неудобства.
29 сентября 2004
Форум обновился до версии 2.0.10
15 мая 2004
Новый раздел: "Программирование"
16 апреля 2004 года
Задачи Ярославского турнира математических боев — 124 задачи с решениями.
29 марта 2004
Таллинская викторина: занимательные вопросы и задачи для увлеченных химией.
1/8 финала. Вариант 3 (8)
Задачи боя "Школа №49 - г.Рыбинск(2)"
15 декабря 2000 года
| Страницы: 1 | |
1. | Даны три положительных числа a, b, c таких, что при любом натуральном k из отрезков длины ak, bk, ck можно составить треугольник. Доказать, что среди чисел a, b, c есть два равных. |
17 Марта 2004 21:27 | |
2. | Решить в целых числах уравнение: 1 + x + x2 + x3 = 2y. |
17 Марта 2004 21:29 | |
3. | На участке, имеющем форму квадрата со стороной 1 км, растет сосновый лес из 4500 деревьев диаметра 50 см. Доказать, что в этом лесу можно выбрать прямоугольную площадку 10м ´ 20м, на которой не растет ни одной сосны. |
17 Марта 2004 21:29 | |
4. | Натуральные числа a, b, c, d таковы, что ab = cd. Докажите, что число (a + b + c + d) не является простым. |
17 Марта 2004 21:29 | |
5. | Доказать, что если n — натуральное число, большее 2, то (1 × 2 × 3 × … × n)2 > nn. |
17 Марта 2004 21:30 | |
6. | Доказать неравенство
|
17 Марта 2004 21:31 | |
7. | Точки A1, A2, …, An не лежат на одной прямой. Пусть P и Q — две такие точки (отличные от точек A1, A2, …, An и не совпадающие друг с другом), что выполняется равенство: A1P + A2P + … + AnP = A1Q + A2Q + … + AnQ = s. Доказать, что существует точка K, для которой A1K + A2K + … + AnK < s. |
17 Марта 2004 21:31 | |
8. | В выпуклом четырехугольнике три тупых угла. Доказать, что из двух его диагоналей большей является та, которая проведена из вершины острого угла. |
17 Марта 2004 21:32 | |
| Страницы: 1 | |