358
476
всего разделов:
активных пользователей:
30 мартра 2005
Форумы снова функционируют.
21 декабря 2004
Видимо в связи с обнаруженными дырами в phpBB, форум был взломан, а через него взломано и всё остальное содержимое ceemat.ru. Всё кроме форума восстановлено, ведется дискуссия по поводу его сохранения.
Приносим извинения за неудобства.
29 сентября 2004
Форум обновился до версии 2.0.10
15 мая 2004
Новый раздел: "Программирование"
16 апреля 2004 года
Задачи Ярославского турнира математических боев — 124 задачи с решениями.
29 марта 2004
Таллинская викторина: занимательные вопросы и задачи для увлеченных химией.
1/8 финала. Вариант 1 (8)
Задачи боя "Школа №36 – Школа №86"
25 ноября 2000 года
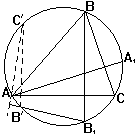
Вписать в данную окружность треугольник АВС, если известны вершина А, направление высоты hА и точка пересечения высоты hB с окружностью. |
Если высоты hA и hB вписанного треугольника ABC пересекают окружность в точках A1 и B1, то вершина C делит дугу A1B1 пополам. Это следует из равенства углов A1AC и B1BC, каждый из которых равен 90° – ÐACB. Построение. Через точку A проводим прямую в данном направлении до пересечения с окружностью в точке A1; пусть B1 — точка пересечения hB с окружностью. Находим середину C дуги A1B1 и проводим AC; проводим B1B, перпендикулярно AC. Треугольник ABC — искомый. Второе решение AB'C' получится, если взять середину C' второй из дуг A1B1. |
17 Марта 2004 21:19 Раздел каталога :: Ссылка на задачу
|