358
476
всего разделов:
активных пользователей:
30 мартра 2005
Форумы снова функционируют.
21 декабря 2004
Видимо в связи с обнаруженными дырами в phpBB, форум был взломан, а через него взломано и всё остальное содержимое ceemat.ru. Всё кроме форума восстановлено, ведется дискуссия по поводу его сохранения.
Приносим извинения за неудобства.
29 сентября 2004
Форум обновился до версии 2.0.10
15 мая 2004
Новый раздел: "Программирование"
16 апреля 2004 года
Задачи Ярославского турнира математических боев — 124 задачи с решениями.
29 марта 2004
Таллинская викторина: занимательные вопросы и задачи для увлеченных химией.
1/16 финала. Вариант 6 (8)
Задачи боя "Школа №42 - Школа №49"
25 ноября 2000 года
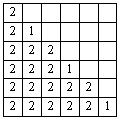
В квадратной таблице N ´ N расставляются числа 0, 1 и 2. При каких N возможно, что среди сумм этой таблицы по строкам и столбцам встретятся все числа от 1 до 2N? |
Пусть S — сумма чисел в таблице. Тогда 2S = 1 + 2 + … + 2N = N(2N + 1). Если число N нечетно, то S — не целое, что невозможно. Если число N четно, то расстановка возможна. На диагонали из левого верхнего угла таблицы в правый нижний расставим попеременно числа 1, 2, 1, 2, …. В клетки таблицы, расположенные левее и ниже рассмотренной диагонали, запишем нули. В клетки, расположенные правее и выше диагонали, запишем двойки. На рисунке показано такое расположение для N = 6. Не трудно показать, что такое расположение чисел удовлетворяет условию задачи.
|
17 Марта 2004 21:06 Раздел каталога :: Ссылка на задачу
|