358
476
всего разделов:
активных пользователей:
30 мартра 2005
Форумы снова функционируют.
21 декабря 2004
Видимо в связи с обнаруженными дырами в phpBB, форум был взломан, а через него взломано и всё остальное содержимое ceemat.ru. Всё кроме форума восстановлено, ведется дискуссия по поводу его сохранения.
Приносим извинения за неудобства.
29 сентября 2004
Форум обновился до версии 2.0.10
15 мая 2004
Новый раздел: "Программирование"
16 апреля 2004 года
Задачи Ярославского турнира математических боев — 124 задачи с решениями.
29 марта 2004
Таллинская викторина: занимательные вопросы и задачи для увлеченных химией.
1/16 финала. Вариант 3 (8)
Задачи боя Школа №86 - Гимназия №1
3 ноября 2000 года
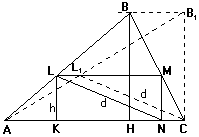
В данный треугольник ABC вписать с помощью циркуля и линейки прямоугольник (две вершины на AC, остальные на BC и AB), имеющий заданную диагональ. |
Для построения достаточно знать высоту h = KL прямоугольника. Пусть прямоугольник KLMN — искомый, KN лежит на AC. Будем перемещать вершину B параллельно AC, сохраняя величину h неизменной, тогда, очевидно, сохранятся величины основания и диагонали прямоугольника. Значит, треугольник ABC можно заменить любым другим с тем же основанием и высотой. Возьмем треугольник AB1C, ÐC = 90°.
Несложно построить CL1 = d, L1 Î AB1, далее строим искомую точку L так, что LL1 параллельно AC. По точке L восстанавливается весь прямоугольник. Смотря по тому, будет ли сторона треугольника AB1C, проведенная из вершины C, меньше, равна или больше данной величины d, задача будет иметь два решения, одно или ни одного. |
17 Марта 2004 17:39 Раздел каталога :: Ссылка на задачу
|