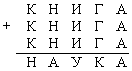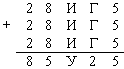358
475
всего разделов:
активных пользователей:
30 мартра 2005
Форумы снова функционируют.
21 декабря 2004
Видимо в связи с обнаруженными дырами в phpBB, форум был взломан, а через него взломано и всё остальное содержимое ceemat.ru. Всё кроме форума восстановлено, ведется дискуссия по поводу его сохранения.
Приносим извинения за неудобства.
29 сентября 2004
Форум обновился до версии 2.0.10
15 мая 2004
Новый раздел: "Программирование"
16 апреля 2004 года
Задачи Ярославского турнира математических боев — 124 задачи с решениями.
29 марта 2004
Таллинская викторина: занимательные вопросы и задачи для увлеченных химией.
Весна 2003 года (25)
Найдите все решения ребуса, в котором одинаковые буквы соответствуют одинаковым цифрам, а разные – разным:
|
Ответ: К = 2, Н = 8, И = 3, Г = 7, А = 5, У = 1. Так как при сложении трех одинаковых цифр А получаем число, оканчивающееся на ту же цифру, то либо А = 0, либо А = 5. Рассмотрим эти варианты. Если А = 0, то Н + Н + Н = 0, или Н + Н + Н = 10, или Н + Н + Н = 20. Первый случай сразу отпадает, так как он возможен только при Н = 0, но разные буквы должны соответствовать разным цифрам. Второй случай (Н + Н + Н = 10) возможен только при Н = 3, при этом одна единица переходит в разряд десятков тысяч, то есть К + К + К + 1 = 3, что невозможно. В третьем случае (Н + Н + Н = 20) значение Н может быть только 6 с переходом двух единиц в следующий разряд. То есть К + К + К + 2 = 6, что опять же невозможно. Если А = 5, то Н + Н + Н = 5, или Н + Н + Н = 15, или Н + Н + Н = 25. Первый случай возможен только при Н = 1, но тогда К + К + К = 1. Этого не может быть. Во втором случае Н = 5, и тогда получим, что А = Н. Остается третий вариант, где значение Н может быть только 8 и К + К + К + 2 = 8, что возможно при К = 2. Таким образом, получаем следующую картину:
Так как при вычислении Г + Г + Г + 1 получаем число, оканчивающееся цифрой 2, то Г + Г + Г оканчивается цифрой 1, то есть Г = 7. Тогда из разряда десятков в разряд сотен переходит две единицы, и, учитывая, что из разряда сотен в разряд тысяч переходит одно единица, получаем, что И + И + И + 2 = 1У. Из неиспользованных цифр для значения И подходит только цифра 3, и тогда У = 1. |
13 Марта 2004 17:43 Раздел каталога :: Ссылка на задачу
|